«Неизвестный Яворский»: фрагмент книги с комментарием Ильдара Ханнанова

Издательство «Композитор» выпускает уникальную двуязычную книгу, в которой фундаментальный труд Болеслава Яворского «Строение музыкальной речи», не переиздававшийся с 1908 года, дополнен множеством его рукописей, публикуемых впервые, и научным комментарием Ильдара Ханнанова. Книга поступит в продажу 21 ноября 2022 года. С разрешения издательства публикуем фрагмент нового издания, предваряемый статьей Ильдара Ханнанова.

Ильдар Ханнанов

Опыт переиздания и перевода «Строения музыкальной речи» Яворского

Болеслав Леопольдович Яворский опубликовал трактат «Строение музыкальной речи» в 1908 году. С тех пор прошло 114 лет, трактат не переиздавался. Идеи Яворского были отражены в труде Сергея Протопопова «Основы строения музыкальной речи», опубликованной в 1930 году. Однако «Основы» — публикация советского времени, со всеми вытекающими особенностями.

Текст книги 1908 года не соответствует академическим нормам нашего времени: в нем отсутствуют важнейшие компоненты, и он не образует завершенного целого. Все, и в России, и на Западе, кажется, слышали о Яворском, но никто не мог с ответственностью утверждать, что знает его, ведь фундаментальный текст-первоисточник отсутствовал. Поэтому возник проект «Неизвестный Яворский». Для его воплощения потребовалось пять лет работы с архивными материалами в Российском национальном музее музыки, усилия Российского музыкального союза, издательства «Композитор» и редакторов — носителей языка. 

Книга Яворского — первый этап в серии переводов первоисточников русской, советской и российской теории музыки на английский язык. Эту идею шеф-редактор издательства «Композитор» Пётр Поспелов предложил в 2018 году. Исполнительный директор Евгения Воронова и генеральный директор Карина Абрамян, президент Российского музыкального союза Андрей Кричевский и директор Российского национального музея музыки Михаил Брызгалов с большим вниманием отнеслись к нашей инициативе и подкрепили ее инвестициями и необходимой для столь монументального проекта организационной работой. В результате на свет появилась книга — 500 страниц на двух языках, с развернутым вступлением, словарем терминов, академическим аппаратом, комментариями, публикацией и переводом текста 1908 года с добавлением более 200 страниц архивных материалов, расшифрованных и оцифрованных, многие из которых изданы впервые.

Яворский и современная теория музыки

Текст книги 1908 года, дополненный архивными материалами, представляет концепцию Яворского во всей полноте, в гетерогенности и инклюзивности ее постулатов. Особенно ярко они проявляются в сравнении с современной западной, и в частности англо-американской, теорией. Необходимо отметить, что идею перевести этот трактат автор обсудил в первую очередь с Ричардом Коном, основателем неоримановской теории, профессором Йельского университета. 

Главный постулат этой теории — так называемая внефункциональная центричность звуковысот. Другими словами, остаются созвучия, созданные традицией, такие как трезвучия, септаккорды и их обращения, но их функции отсутствуют. При этом главным критерием осмысленности музыки представляется экономное — «парсимониальное» — голосоведение. 

Яворский, разрешая неустои исключительно по полутонам, придерживается такого же принципа. Но его подход прямо противоположен неоримановскому: по Яворскому, функции остаются, а центральные созвучия перестают главенствовать. Его концепцию можно вкратце сформулировать как «функциональную ацентричность звуковысот». Во всяком случае, диалог с неоримановской теорией, да и с трансформативной, представленной Дэвидо Люеном, гарантирован.

Сторонникам трансформативной и неоримановской теорий голосоведение представляется как некая карта, или сеть, — Tonnetz (нем. — тональная сеть). Термин этот употребил в своих поздних трудах Хуго Риман, но схожие схемы можно найти и у Готфрида Вебера, и у Николая Андреевича Римского-Корсакова (степени родства тональностей). Дмитри Тимошко представил ряд геометрических фигур, которые отображают, по его мнению, тональное пространство. В этой связи спиралевидные схемы Яворского вписываются в идею тональной сети, но представляют совершенно новый, не исследованный в неоримановской теории вариант. Обращает на себя внимание бесконечность спирали — по контрасту с замкнутостью тональных сетей у Тимошко и Кона. Элементы сети — не трезвучные, а тритоновые.

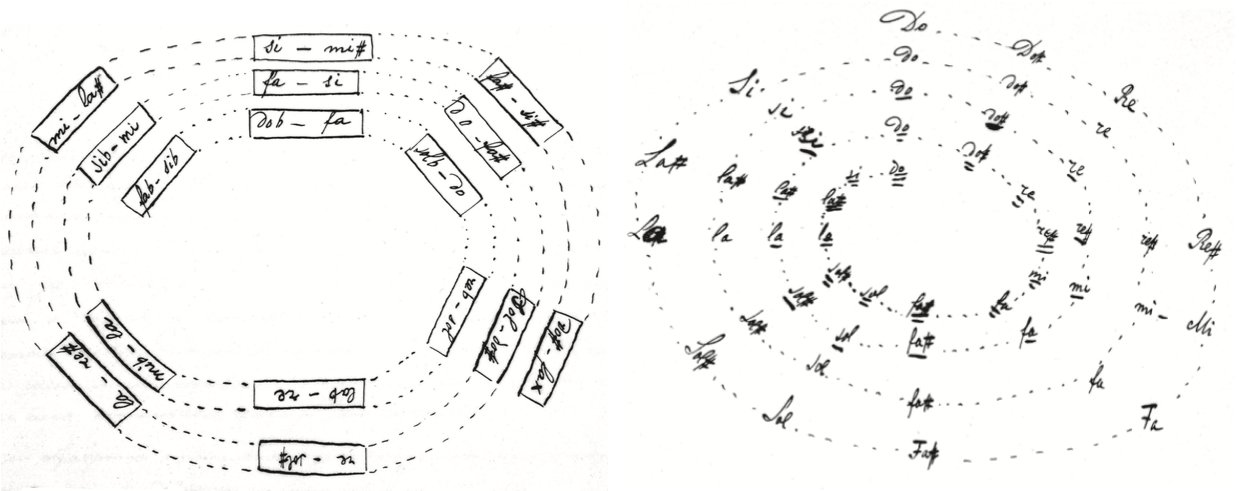
«Неизвестный Яворский», с. 249, 251

Когнитивные аспекты

Особенностью концепции Яворского является ее опора на восприятие и на его энергетику. Естественнонаучные по своей сути термины — «устой», «неустой», «сопряжение», «тяготение», «момент» — в приложении к категориям восприятия, безусловно, обновят лексический аппарат музыкальной когнитивистики и вызовут большой интерес со стороны таких ученых, как Фред Лердал и Кэрол Крумхансл. Необходимо отметить, что современная теория опирается в большинстве случаев только на простейшую часть математики — теорию множеств и групп, а Яворский использовал термины из области физики, как и Жан-Филипп Рамо. Вероятно, современным теоретикам музыки стоит вернуться к физике и таким категориям высшей математики, как «функция», «дифференциальное исчисление» и «математическая топология». Первые пять страниц архивных материалов Болеслав Леопольдович посвящает обсуждению некоторых научных универсалий («отношение», «кратность», «прогрессия» и так далее). По уровню абстрагирования этот раздел, пожалуй, не имеет равных в теориях XIX–XX веков. Кратными, например, оказываются не только доли метра (что легко представить в простейшей арифметической форме), но и тональности в произведении.

Термины теории новой музыки

В архивных материалах представлены более основательные и точные формулировки, чем в «Строении музыкальной речи». Так, на листе 243/4 Яворский дает определение категории ряда:

РЯДЫ

Ряд величин, составленных по какому-нибудь определенному

закону или принципу, называется вообще рядом.

Сопоставление одинаковых (а а) или различных (a b c d) величин.

Фонд 146, ед. хран. 243, лист 4; «Неизвестный Яворский», с. 224

Ряд — основа перехода от тональной к атональной музыке; слово принято относить к теории новой музыки Арнольда Шёнберга 1920-х годов, Юрий Николаевич Холопов часто употреблял его в лекциях и публикациях. Процитированное выше определение фактически подтверждает, что этот термин был введен в теорию музыки и осмыслен в наиболее универсальной форме Яворским до 1908 года. 

В его архиве находится рукописная книга 1901 года объемом 200 страниц, которая содержит множество рядов и их описания. Впрочем, термин «ряд», по Яворскому, можно применять как к атональной, так и к тональной музыке — без преодоления водораздела между ними. Этим теория новой музыки Яворского отличается от последующих, радикальных и часто плохо обоснованных нововведений. Для Яворского просто не существует трагической границы между старой и новой системами. В основе любой музыки находится отношение неустоя к устою, как в звуковысотном выражении, так и в метроритмическом.

Форма

Пожалуй, главное преимущество теории Яворского перед западными аналогами заключается в ее целостности и одновременно разнородности. Когда Яворский рассуждает о звуковысотности, естественно и органично возникает необходимость описывать метрический аспект — предыкт и икт (слабая и сильная доли в традиционной терминологии). А когда он пишет о разделах формы, то ставит их в зависимость от гармонических устоев и неустоев. Знаменательны в этом отношении схемы классических форм Яворского: от интонации — к обороту и фразе, предложению, периоду и песне:

«Неизвестный Яворский», с. 333, 335, 337; схемы форм

Такие схемы распространены и в современных учебниках, однако у Яворского сегменты форм определяются балансом устоя и неустоя — это объясняет их конституцию.

Яворский и Риман. Объединение разнородных параметров

Идею объединения разнородных параметров в единой модели формы-гармонии-метра Яворский унаследовал от Хуго Римана, в частности исходя из его идеи метрического восьмитакта. Здесь уместно вспомнить, что в результате уничтожительной критики Генриха Шенкера теория музыки наших дней полностью избавилась от учений Римана и многих других выдающихся теоретиков XIX века. Иначе как выстрелом себе в ногу это назвать невозможно. А Яворский увидел возможность переноса старой идеи на новый атональный материал.

Кстати, в США были попытки создать «теорию всей музыки». Так, например, называется книга Джея Рано («A Theory for All Music»), но в ней автор пытается привести все богатство музыкальной традиции к своему весьма ограниченному аппарату: «теории рядов» и «теории конечных множеств», с включением некоторых идей о «голосоведении и контрапункте». 

Создать унифицированную теорию всей музыки трудно, и, пожалуй, невозможно без континентальной консерваторской традиции XIX века. Иначе получается «мыльный пузырь», невольно отсылающий к рассказу Шукшина «Срезал!». Яворскому удалось создать унифицированную теорию благодаря тому, что он получил фундаментальное доуниверситетское музыкальное образование в училище Императорского российского музыкального общества.

Гармония

Одной из фундаментальных ошибок англоязычной теории музыки XX века был отказ от категории гармонии, и в частности от идеи тонально-гармонической функции. И шенкеровская теория, и теория рядов Бэббита — Форта (также известная как сет-теория), и концепция октатоники, и неоримановская, и даже новейшая теория схем — партименто, — все дружно и в один голос отменяют функциональный синтаксис. В Предисловии к английскому переводу «Учения о гармонии» Шенкера его ученик и последователь Освальд Йонас пишет, что из-за «порочной теории Рамо музыка пошла по ложному пути».

 Отличительной особенностью русской, советской да и современной российской традиции является сохранение идеи гармонии в ее функциональной интерпретации. Теория новой тональности Юрия Николаевича Холопова сохраняет идею функции. В этом он следует заветам Яворского, который применил идею функции к новой системе тритонового эквилибра, выходящей далеко за пределы квинтового синтаксиса классической тональности. Так же как и Холопов, Яворский в свое время предложил новые интерпретации и даже новые названия функций. Так, бросается в глаза новый символ, который издательство «Композитор» поместило на обложку книги:

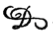
«Неизвестный Яворский», с. 34

Новое тональное пространство Яворского структурировано тритоновыми связями — они подобны украшениям на новогодней елке, только расположены на расстоянии парсеков от нашей планеты. В столь отдаленном космосе возможны соединения местных топологий. Так, доминантовое направление — движение по спирали — соприкасается (или «склеено», по терминологии Дмитри Тимошко) с субдоминантовым. В точке соприкосновения образуется соединительная функция DS. В тональной музыке она выражена аккордами на шестой низкой ступени, в частности аккордами с увеличенной секстой.

«Неизвестный Яворский», с. 193

Вот, кажется, и нашелся ответ на вопрос, как интерпретировать аккорды с увеличенной секстой — как производные от доминанты (двойная доминанта) или от субдоминанты. Училищные споры московской и петербургской школ разбивает соломоново решение Яворского.

Голосоведение

В «аккордовых геометриях» Тимошко тональное пространство представлено просто как набор нотных знаков. В этой теории нет места функции — тому, что Рамо обозначал как sous-entendu — неслышимое, но подразумеваемое. У Яворского же сталкиваются две спирали: доминантовая и субдоминантовая, и обе они sous-entendu. Человеку без музыкального образования невозможно увидеть их в нотах — необходимы годы профессиональной эволюции слуха: от тона к интервалу, от интервала к аккорду и далее, к высшей ступени эволюции — к функции.

При этом критики функциональной теории, с их главным аргументом — все решает голосоведение, — будут разочарованы высказыванием Яворского, обнаруженным на листе 2456.3 в фонде 146:

Когда говорят, что контрапункт предшествовал гармонии,

то говорят ерунду, так как всему предшествовала, сопутствовала,

следовала и главенствовала форма, т. е. ритм лада во времени,

т. е. то, что на самом деле есть гармония.

«Неизвестный Яворский», с. 490

Таким образом, Яворский ставит гармонию во главу угла и выводит ее из формы. 

Музыкальная семиотика

Яворский не забывает и о семиотике. Его определение интонации в частости и музыкальной речи в целом исключительно точно в техническом отношении и максимально всеохватно в гуманитарном и междисциплинарном ракурсах. В архиве содержится статья о музыкальной речи — философское размышление о ее характере, лишенное каких-либо композиционно-технических аспектов. 

Милтон Бэббит (один из создателей теории рядов) весьма самодовольно декларирует, что музыка «самореферентна». Это можно расценить как попытку обойти существование ничего не выражающей музыки. Но правда прорывается сквозь любые преграды: музыка не только не самореферентна, она — источник самой сильной, всепоглощающей и всепроникающей референтности. С первым звуком мы слышим целую плеяду осознанных или подсознательных аллюзий, и в этом отчасти заключается значение музыки.

Интонация, икт и предыкт

Интонация — центральная и основополагающая категория теории Яворского. В отличие от многих «мыльных пузырей» в современной музыкальной теории, она вбирает в себя весь опыт музыкальной композиции прошлого, обобщая ее важнейшие элементы. Идея мотива в музыке и других искусствах впервые была представлена в словаре Себастьяна де Броссара и позже у Жан-Жака Руссо в середине XVIII века. В учении Адольфа Маркса и трудах Антонина Рейхи сложилось узкое, техническое понятие музыкального мотива. Французское le mot отсылает к слову (к тому единственному слову, которое заключает в себе смысл всего произведения), итальянское mottivo уже предполагает физический элемент. Именно его Яворский обозначил как динамическое и логическое начало в его простейшей форме — предыкта и икта (здесь можно усмотреть влияние метроритмической теории Римана). Интонация, по Яворскому, разнородна, но цельна и синтезирует понятия звуковысотной структуры (тритон с разрешением) и метроритмическое взаимоотношение «предыкт — икт» (слабая доля — сильная доля). Функциональная иерархия музыкальных тонов в интонации определяется их метрическим положением, а метрическая структура создается следованием неустоя в устой или устоя в неустой. В своем определении Болеслав Леопольдович не ограничивается структурным аспектом интонации, рассматривая ее как основной элемент вербальной речи.

Речь

Следовало обратиться к этому термину в самом начале статьи. Его широкое распространение и нейтральность может отбить желание читать первую страницу трактата, но именно она содержит основу теории Яворского и подлежит специальному анализу. Яворский не ссылается на существующую литературу, а его стиль и язык афористичны. Возможно, Болеслав Леопольдович, как и многие другие, пал жертвой обаяния Фридриха Ницше.

Всякое проявление жизни может служить содержанием человеческой речи,

которая имеет два вида — звуковой и пластический.

Музыкальная речь, одна из составных частей звуковой речи,

черпает свой (состав) материал и законы из той же жизни,

проявлением которой она является.

Материалом, из которого создается музыкальная речь

(музыкальный ее состав), является звук во времени. 

«Неизвестный Яворский», с. 92

В этом абзаце — звено, соединяющее теорию музыки и ее вероятное происхождение, это монументальная генеалогия, сходная с предложенной Мишелем Фуко. Следуя нити Ариадны, пойдем от частного к общему. Основа музыки — звук, столь сильно занимающий современных исследователей, — существует исключительно в контексте времени. Другими словами, теория музыкального ритма невозможна вне идеи гармонии, также как гармонию нельзя отделить от метроритмического процесса. Здесь Яворский наследует одно из главных достижений Римана, центральное для всей музыкальной теории последних столетий, — теорию метрического восьмитакта. Сделав еще один шаг, можно обнаружить, что и это весьма абстрактное определение не завершено: звук во времени есть не сущность музыки, а только лишь ее материал. Суть музыки — воплощение человеческой речи. 

Может показаться, что рассуждения о музыкальной речи — сугубо русская или советская прерогатива. И правда, Одоевский, Стасов и Серов об этом писали, Мусоргский охотился за речевыми интонациями, а Яначек записывал напевки — в Восточной Европе была такая мода. Но музыкальная речь являлась целью анализа и для немецкой теории музыки XVIII века, ее даже обозначали как Klangrede. Несмотря на полный отказ современных композиторов от отражения живой человеческой речи в своих сочинениях, этот вопрос остается открытым. Ведь без аналогии с вербальными структурами музыка замедляется и перестает развиваться. В конце концов, речь — одно из проявлений жизни.

Болеслав Яворский

Архивные материалы из фонда 146

Первая публикация

Вступление

Внешняя человеческая речь двусоставна, она является одним из проявлений жизни быть двоякого рода — звуковой и пластической. Всякое проявление жизни может служить содержанием человеческой речи, которая имеет два вида — звуковой и пластический.

Музыкальная речь, одна из составных частей звуковой речи, черпает свой (состав) материал и законы из той же человеческой жизни, проявлением которой она является.

Материалом (составными частями, элементами), из которого создается музыкальная речь, и является звук и время.

Звук

Сущность звука, его состав и взаимоотношения звуков между собой еще не исследованы. Изучение ограничивается составом одного звука, производимого мертвым телом (струной, камертоном и т. п.) и построением ряда звуков на основании математических вычислений, а не на основании соотношений и взаимодействий звуков живых, воспроизводимых живыми существами.

Звук производит самое разнообразное впечатление в зависимости от условий его воспроизведения.

Первое впечатление, которое производит звук, есть высота звука, его окраска (тембр) и вид самого звука — его гласность (звучание на определенный гласный звук, которому могут предшествовать или за которым могут следовать согласный звук) или безгласность.

Второе впечатление есть сила звука, динамика (греческое δύναμις — сила), способы его воспроизведения (legato — постепенное незаметное воспроизведение и исчезновение отдельного звука, non legato — определенное точное по моменту начало и конца звука, и staccato — толчкообразное начало и конец звука) и держания (ровный прерывистый, p.f. crescendo, decrescendo, subito (p.f )).

Время

Музыкальная речь является не памятником прожитой жизни, а проявлением самой жизни, жизни совершающейся, длящейся во времени, и время — необходимое условие существования, является второй составной частью музыкальной речи.

Законы

Законами, располагающими звуки во времени, являются законы отношений. Отношение есть результат, поученный от сравнения однородных величин.

I. Аналогия (соответствие, подобие):

А) прямая (простая) — периодичность — последование явлений или отношений:

1) разных, например: а b c d e f g,

2) одинаковых: а а а а,

3) одинаковых через определенный промежуток явлений или отношений:

а b а c а d а c а, и а b а с а d а c а,

4) двойная периодичность, периодичность совокупности разных явлений или отношений: аа аа или аb аb аb, или аbc аbc аbc;

Б) обратная — симметрия — соотношение (явлений) в порядке, при котором крайнему соответствует крайнее, среднему среднее:

1) простая симметрия аb ba или abc cba,

2) двойная симметрия в частях симметричного целого (ab ba) (ba ab).

Всякая симметрия со своим обратным составляет самоопределяющуюся форму.

Симметричные части не должны непременно соприкасаться; симметрия может быть и на расстоянии.

Случаи соединения периодичности и симметрии: Например, a b с d c e a

1. Периодичность целого при симметрии в частях: (ab ba) (ab, ba).
2. Симметрия целого при периодичности в частях: (ab, ab) (ba, ba).

II. Отношения по величине: 

= равенство

Отношения арифметические:

≷} одна величина больше или меньше другой на какую-нибудь величину.

Отношения геометрические (знаменатель всегда число отвлеченное):

одна величина:

1) больше или меньше другой, вдвое, втрое, вчетверо и т. д., или

2) относится к другой, так как 2:3; 3:2; 3:4; 4:3; 2:5 и т. д.

Зависимость частей от целого, причин от следствия.

III. Кратность:

Отношение причин к следствию, равенство противодействия действию.

Наименьшее кратное, наибольший делитель, арифметический остаток.

IV. Пропорциональность:

Пропорция есть равенство двух отношений (арифметических или геометрических); всякая пропорция имеет восемь видов (можно переменить имена крайних членов, потом имена средних, наконец места тех и других вместе, средние сделать крайними и наоборот).

В арифметической пропорции суммы крайних членов равна сумме средних. Арифметическая середина (средняя величина) есть такая величина, которую получили, разделив сумму данных величин на число их.

В геометрической пропорции произведение крайних членов равно произведению средних.

Если в геометрической пропорции средние члены равны (среднепропорциональны), то пропорция называется непрерывной. Обратной пропорцией называется обращение данной. Первоначальная пропорция со своей обратной составляет самоопределяющуюся форму.

V. Прогрессия:

Прогрессия есть ряд величин (отношений), неравенство возрастающих и уменьшающихся по предписанному принципу отношений, из которых каждая последующая получается из предшествующей:

1) прикладывая к ней одно и то же количество (разность прогрессии) или последовательный ряд производных одного количества на 2, 3 и т. д. (арифметическая прогрессия);

2) через умножение на одно и то же количество (знаменателей прогрессии) (геометрическая прогрессия).

Когда абсолютная величина членов вырастает, то прогрессия называется вырастающей, когда эта величина уменьшается, — убывающей.

Обратной прогрессией называется обращение данной прогрессии, причем из убывающей прогрессии получается вырастающая, и наоборот.

Первоначальная прогрессия со своей обратной составляет самоопределяющуюся форму. Нисходящая прогрессия, доведенная до единицы отношения, составляет самоопределяющуюся форму.

Сумма членов арифметической прогрессии, равноотстоящей от начала и конца ее, есть величина постоянная, равная сумме первого и последнего членов.

Сумма членов арифметической прогрессии равна сумме крайних членов, умноженной на половину числа членов.

Сумма всех членов геометрической прогрессии равняется дроби, числитель которой есть разность между произведением последнего члена на знаменатель и первым членом, а знаменатель есть знаменатель прогрессии без единицы.

Убывающая прогрессия, продолжающаяся до бесконечности, называется бесконечно нисходящей прогрессией.

Сумма бесконечно нисходящей прогрессии равняется первому члену, деленному на единицу без знаменателя.

Ряды

Ряд1 величин, составленных по какому-нибудь определенному закону или принципу, называется вообще рядом. Сопоставление одинаковых (а а) или различных (a b c d) величин.

Выбор из определенного числа элементов некоторых и сопоставление их в известном порядке может быть троякого рода: размещения, перестановки и сочетания2.

I. Размещение:

Размещением называется соединение из определенного числа величин (элементов) в определенном порядке.

Например, размещение из чисел, величин элементов: a, b и с, или по два: ab, ba, ac, ca, bc, cb.

Число размещений из элементов m величин элементов по n равняется произведению n последовательных уменьшающихся чисел, начиная с m.

II. Перестановка:

Перестановкой называется соединение, составленное из всех данных элементов в определенном порядке.

Например, перестановка из трех величин: a, b и с: abc, acb, bac, bca, cab, cba.

Число перестановок из m элементов равно произведению m первых чисел.

Когда некоторые из данных элементов равны, то перестановки называются перестановками с повторениями, например, aaab, aaba, abaa, baaa.

III. Сочетание:

Сочетанием называется соединение из определенного числа элементов, независимое от порядка этих элементов. Например, сочетание из трех элементов a, b и с по два ab, ac, bc.

Число сочетаний из m элементов по n равняется (числу сочетаний) произведению n последовательных уменьшающихся чисел, начиная с m, деленного на произведение первых чисел.

Логическое развитие3 есть применение сил ума к целесообразности и содержательности построения и содержания музыкальной речи.