Вокруг творчества Янниса Ксенакиса (1922–2001) сложилась богатая литература, тон которой задал сам композитор своим тракта­том «Формализованная музыка» [19; 18; 3]. Пишущие о Ксенакисе в большинстве своем развивают и комментируют положения этого трактата, воспроизводя рассыпанные по нему математические формулы и схемы или обходясь без математики и стараясь разъяснить запечатленные в формулах теоретические основы искусства композитора более или менее общепонятными словами. Такой подход оправдан, но в нем угадывается оборотная сторона: чрезмерная опора на то, что писал о своей музыке сам Ксенакис, не всегда помогает адекватной характеристике его стиля и композиторского метода.

Допуская некоторое преувеличение, мож­но сказать, что все зрелое творчество Ксе­на­киса, «как дуб в желуде», содержится в его первом (не считая ранних опытов) и доныне самом популярном опусе — «Metastasis» для 61 инструменталиста (1954). Одно из возмож­ных толкований заглавия этой семиминутной пьесы (μετά+στάσις) — «после покоя». По смыслу оно применимо едва ли не к любому традиционному музыкальному произве­дению, где начальная тоника символизирует исходный «стасис», а все дальнейшее есть не что иное, как «метастасис». В партитуре Ксенакиса начальному состоянию покоя соответствует унисон 46 струнных pianissimo на ноте g; далее инструменты, один за другим, выходят из этого состояния, крещендируя и глиссандируя в разных направлениях до достижения многозвучного кластера for­tissimo. Ближе к концу, после нескольких насыщенных разнообразными движениями разделов и генеральной кульминации, поме­щенной около точки золотого сечения, тот же кластер воспроизводится pianissimo; отходящие от него glissandi несколько более сложной конфигурации, чем в начале, ведут обратно к стасису, и целое завершается унисо­ном всех струнных diminuendo на ноте gis.

В самом общем плане композиция «Me­ta­­stasis» реализует глубоко традиционную центробежно-центростремительную модель целостной музыкальной композиции (разни­ца в полтона между начальным g и за­вер­­шающим gis не противоречит общей цент­ро­бежно-цент­ростремительной логике). Но с му­зыкально-исторической точки зрения «Meta­sta­­sis» примечателен не столько своей от­но­си­тельной традиционностью, сколько тем, что здесь укоренены некоторые принци­пиаль­ные художественные открытия Ксенакиса. Наиболее заметными индикаторами нова­тор­ского стиля композитора выступают массовые glissan­di, уводящие от стасиса в начале пьесы и возвращающие к нему в конце. Компле­мен­том по отношению к массовым glissan­di выступают индивидуализированные звуковые события разного масштаба: разбро­санные в пространстве отдельные звуки, более или менее протяженные связные линии из звуков определенной высоты, короткие групповые (но не массовые) glissandi-«мазки» [13, 73]. Для обозначения подобных обоб­щенных типов презентации звучащего мате­риала Ксенакис ввел термин «звуковые сущности (êtres sonores)» [19, 16 ff]. Фактически он синонимичен термину изобретателя кон­кретной музыки Пьера Шеффера «му­зыкаль­ные объекты» [10], под которыми подразумеваются звучания как таковые, в равной степени музыкальные и немузыкальные, абстрагированные от своих источников, ха­рак­теризуемые определенным набором пара­метров — таких, как изменение массы, из­ме­нение высоты, динамический и тембровый профиль, — и выступающие в качестве исходного («конкретного») материала для ком­позиции. Далее оба термина будут использоваться как взаимозаменяемые.

После «Metastasis» Ксенакис всерьез при­ступил к «математизации» своего творче­ства, и его разъяснения собственных творческих принципов и отдельных опусов изо­билуют формулами, смысл которых абсолютно недоступен подавляющему большинству гуманитариев. Вместе с тем мы вряд ли ошибемся, если предположим, что за ними кроется не столько научный (в современном смысле) склад мышления, предполагающий структурирование материала на заранее разработанной математической основе, сколько стремление художника, увлеченного натурфилософией, обосновывать свои концепции с помощью аналогий из области естественных и точных наук1. Придерживаясь натурфилософского подхода, попробуем сформулировать некоторые закономерности, выяв­ляемые в «Metastasis», важные для творчества Ксенакиса в целом и, возможно, имеющие также более широкое значение.

По-видимому, не следует специально до­казывать, что многие привычные музыкально-тео­ретические категории — такие, как мелодия, гармония, полифония, тематическое развитие, — в основном мало пригодны для характеристики большей части «сущностей», с которыми работает Ксенакис. Для его музыкальных объектов и их конгломератов, на наш взгляд, более значимы следующие параметры, разносторонне характеризующие композиторское «изделие» как эмпирически наблюдаемый феномен с особым набором дифференциальных признаков, уникальным образом распределенных во времени и пространстве:

1. Прозрачность, она же внятность, она же «прослушиваемость» объекта или конгломерата. Антонимы — густота, плотность, вязкость.

2. Информативность, или «событийность» — мера присутствия в объекте или конгломерате звуковых конфигураций (со­бы­тий) с отчетливо выраженными, рельефными, обращающими на себя внимание индивидуальными признаками. Антонимы — бессобытийность, «смазанность» контуров, монотонность.

3. Интенсивность — мера непосредственного физиологического воздействия, «драйва»2, определяемая такими моментами, как уровень громкости, яркость колорита, кинетическая активность элементов, входящих в состав объекта или конгломерата. Антонимы — ослабление напряженности, релаксация.

Теоретически каждый из трех парамет­ров может быть измерен; для этого следует систематизировать все множество фигурирующих в партитуре объектов, вывести для каждого из них количественный показатель, рассчитанный по совокупности характеристик, зафиксированных в нотных знаках и диакритике (динамических и темповых указаниях, знаках артикуляции и тому подобное), и проанализировать распределение показателей в синхронии и диахронии для получения объективных данных по взаимодействию и динамике всех трех параметров. Однако точные измерения в данном случае едва ли могут быть продуктивны: во-первых, для них нужен непомерно громоздкий математиче­ский аппарат, и, во-вторых, они заведомо не способны обогатить наши представления об эстетических достоинствах музыки (нет нужды специально подчеркивать, что значения показателей сами по себе эстетически нейтральны). Вместе с тем и без точных вычислений достаточно ясно вырисовывается следующая триада законов, регулирующих отношения между параметрами (оговоримся, что, поскольку речь идет не о явлениях природы, а о продуктах человеческого творчества, строгость этих законов относительна):

Закон № 1. При неизменной интенсивности информативность прямо пропорциональна прозрачности. С утратой прозрачности индивидуальность событий нивелиру­ется и уровень информативности снижается: так, информационная ценность дискретного объекта (звука, конгломерата, «мазка» и тому подобное) в составе звукового облака тем больше, чем меньше густота последнего.

Закон № 2. Если уровень информатив­ности остается неизменным, то интенсивность обратно пропорциональна прозрачности. Это значит, что из двух отрывков, содержащих одинаковое число событий, более высоким показателем интенсивности характеризуется тот, где эти события спрессованы в более густой фактуре.

Закон № 3. При неизменной прозрачности информативность нарастает параллельно интенсивности. Чтобы убедиться в справедливости этого закона, достаточно сопоставить некоторые моменты «Metastasis» — например, тремолирующий кластер fortissimo
в начальном разделе и тот же кластер pia­nissimo ближе к концу, извилистые glissandi в конце и прямолинейные glissandi в начале, — по таким «неточным», но интуитивно понятным критериям, как музыкальная содержательность и сила непосредственного воздействия.

Натурфилософские корни выведенных закономерностей подтверждаются тем, что они изоморфны трем физическим законам, описывающим поведение фиксированной массы идеального газа. Чтобы в этом убедиться, достаточно подставить на место наших трех параметров — прозрачности, информативности и интенсивности — три параметра, характеризующих состояние идеального газа, а именно: объем, давление и температуру.

Напомним самую общую суть этих законов, изучаемых в школьном курсе физики.

1. Закон Гей-Люссака: при постоянном давлении занимаемый газом объем возрастает пропорционально температуре.

2. Закон Бойля — Мариотта: при постоян­ной температуре давление газа обратно пропорционально занимаемому газом объему.

3. Закон Шарля (он же второй закон Гей-­Люссака): при постоянном объеме давление газа прямо пропорционально температуре.

«Идеальный газ» — чисто теоретический конструкт, в реальности же все три «газовых» закона соблюдаются более или менее приблизительно, поскольку на действие каждого из них в той или иной мере влияет контрдействие двух других законов и вмешательство сторонних факторов. То же можно сказать и о сформулированных выше законах № 1, 2 и 3. Как бы то ни было, язык Ксенакиса приспособлен для того, чтобы следовать им достаточно строго. Во-первых, музыке Ксенакиса не свойственны длительные (как у «минималистов») остинато, секвенции и другие многократные повторы, неизбежно снижаю­щие информационную значимость повторяемых сегментов при неизменном уровне прозрачности/плотности, и тем самым нарушающие закон № 1. Во-вторых, в его языке не действует система гармонических напряжений/релаксаций, не зависящих от уплотнений и разрежений фактуры и, следовательно, безразличных к закону № 2 (данный пункт относится, вообще говоря, к любой музыке, не основанной на функциональной гар­монии). Наконец, в музыке Ксенакиса не встре­чаются иностилевые включения, существенно повышающие показатель информативности без изменения или даже при понижении интенсивности и, следовательно, противоречащие закону № 3.

***

В литературе о Ксенакисе встречается термин «трансфер», указывающий на перенесение научных идей и концепций в область музыки [11, 1062]. Трудно сказать, имел ли Ксе­накис в виду трансфер трех конкретных «газовых» законов или их внутренняя связь с его композиционными методами обусловлена натурфилософской интуицией более общего порядка. Но можно с уверенностью утверждать, что физика газов занимала его как источник идей для художественного воплощения процессов, происходящих с ог­ром­ными массами мельчайших единиц. Во вся­ком случае, концепцию своего следую­щего опуса — «Pithoprakta» для двух тромбонов, 46 струнных, ксилофона и вудблока (1955–1956) — композитор возводит к закону Макс­велла — Больцмана, описывающему распре­деление скоростей частиц (молекул, атомов) идеального газа. В «Формализованной музыке» приводится короткий отрывок «Pitho­prakta» с соответствующим графиком и комментарием; он составляет меньше одного процента общего объема пьесы, и вопрос о том, насколько все остальное также имеет отношение к данному физическому закону, остается открытым. При этом триада законов, сформулированных чуть выше, выполняется в «Pithoprakta» неукоснительно.

Слово πιθοπρακτά — неологизм Ксенакиса — может быть переведено как «вероятностные действия» (очевидно, имеется в ви­ду вероятностное моделирование поведения частиц). Отныне такие действия становятся для Ксенакиса обычной практикой. В 1957 году он выступил со статьей о «вероятностной» — в его терминологии «стохастической» (от древнегреческого στοχαστικός — «умеющий верно угадывать») — музыке. Один из разделов статьи посвящен систематизации основных этапов музыкальной композиции. Вкратце она сводится к следующему: на стадии «макрокомпозиции» определяется общая логическая канва целого и осуществляется отбор звуковых сущностей; на стадии «микрокомпозиции» устанавливаются функциональные и вероятностные отноше­ния между сущностями (соответственно «ал­гебра вне времени» и «алгебра во времени»); затем полученная система отношений приводится в действие в рамках макрокомпозиционной схемы, наполняя ее реальной му­зыкальной субстанцией и, возможно, корректируя ее [19, 33–34].

По-видимому, первым произведением Ксенакиса, созданным согласно этому алгоритму, стал «Achorripsis» для 21 инструмента (6 деревянных духовых, 3 медных, 3 ударных и 9 струнных без альтов; 1957). Возможный перевод заглавия — «разбрасывание звуков». В трактате «Формализованная музыка» автор подробно, с привлечением математического аппарата, способного оказать гипнотизирующее воздействие на среднего читателя, последовательно описал использованные в «Achorripsis» принципы «разбрасывания звуков». Перескажем описанный им путь от замысла к его осуществлению в самых общих чертах, опуская формулы, таблицы и графики3.

Логическую канву пьесы составляет распределение Пуассона, выражающее вероятность некоторого числа однотипных событий в течение конечного промежутка времени, если эти события происходят с известной средней частотой независимо друг от друга. Для реализации идеи избраны семь типов звуковых сущностей, получивших следующие условные названия: «флейта» (пикколо, малый кларнет, бас-кларнет), «гобой» (гобой, фагот, контрафагот), «glissando» (струнные), «ударные» (ксилофон, вудблок, большой барабан), «pizzicato» (струнные), «медь» (2 трубы и тромбон), «arco» (струнные). Продолжительность и объем пьесы — 7 минут, 182 такта на ²/₂, в темпе = 52; целое складывается из 28 пятнадцатисекундных сегментов объемом по 6,5 тактов.

События, подлежащие распределению по закону Пуассона, делятся на пять типов: нулевые, единичные, двойные, тройные и четверные. По мнению Ксенакиса, обычный оркестр способен сыграть 10 звуков в секунду, но для своего ансамбля композитор устанавливает более «щадящую» норму — 2,2 звука в секунду, что соответствует 5 звукам в такте и 32,5 звукам в 6,5 тактах; эти цифры характеризуют среднестатистическое единичное событие. Двойное, тройное и четверное события характеризуются цифрами в 2, 3 и 4 раза бóль­шими; нулевое событие — отсутствие звуков.

Венец этапа макрокомпозиции — матрица «Achorripsis» (см. пример 1; цит. по [15, 49]). В каждой из ее 28 × 7 = 196 ячеек отражена мера «событийности» того или иного из се­ми объектов в пределах того или иного из 28 оди­наковых по продолжительности сегментов пьесы. Нулевых событий всего 107; единичных, двойных, тройных и четверных, соответственно, 65, 19, 4 и 1. Разброс этих значений достаточно точно соответствует формуле Пуассона, выражающей рост вероятности события от наиболее ожидаемого (здесь — нулевого) к наименее ожидаемому (четверному). Цифры внутри «ненулевых» ячеек указывают на среднее число звуков в такте. Для единичных, двойных и тройных событий это число колеблется, соответ­ственно, от 2,5 до 6,5, от 8,5 до 11 и от 14 до 17 при «нормальных» значениях 5, 10 и 15, а у единственного четверного события оно равно 20.

Пример 1

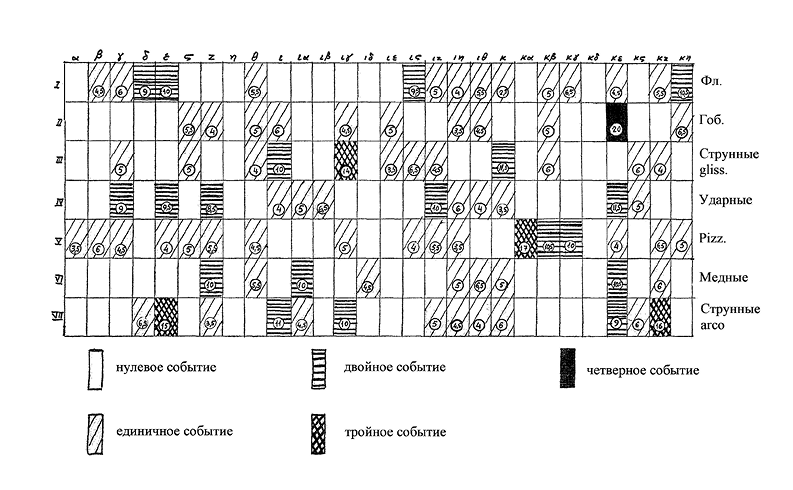
На этапе микрокомпозиции определя­ются правила, регулирующие отношения меж­ду звуками внутри событий: алгебра во вре­мени (отношения длительности), ал­геб­ра вне времени (отношения высоты) и осо­бый род алгебры, которому композитор уде­ляет особое внимание, — конфигура­ция и ско­рость glissandi. Этот последний род удостаи­вается весьма детального математи­ческого анализа, тогда как о других «микрокомпозиционных» связях и корреляциях Ксе­накис предпочитает не говорить, поскольку это было бы «слиш­ком долго, сложно и запутанно» [19, 47].

В конце раздела об «Achorripsis» Ксенакис задается следующим вопросом: «Сохранит ли эта музыка эффект неожиданности после некоторого множества прослушиваний? Не превратится ли она, благодаря запоминанию, в ряд предсказуемых явлений, несмотря на то, что частота событий определяется законами случайности? (курсив Ксенакиса. — Л. А.)». Его ответ гласит: 

<…> распределение событий пока­жется случайным только при первом прослушивании. Но затем, по мере повторных прослушиваний, связи между событиями, распределенными «случайным» образом, сформируют структурную решетку, которая приобретет определенный смысл в сознании слушателя, и стимулируют особого рода «логику», новую систему связей, способную удовлетворить как его интеллектуальные, так и его эстетические запросы (конечно, если у автора есть дарование) [19, 47].

Характерно, что, казалось бы, самое главное условие привлекательности музыки — наличие у автора художественного дара — сформулировано здесь в скобках, как нечто заведомо менее существенное, чем непредсказуемость, подчиненная некоей особой логике, обнаруживающей себя только при многократном слушании. Вопрос о том, насколько увлекательна задача уловить эту логику, способна ли она стимулировать долгосрочный интерес слушателя к этой музыке, остается открытым.

Скептическое отношение к процитиро­ван­­ному рассуждению подкрепляется тем, что матрица «Achorripsis» сама по себе не об­­ла­дает особой внешней привлекательностью (она может ассоциироваться с образ­цами сравнительно безыскусной табличной нотации Мортона Фелдмана наподобие «Пере­се­чений», 1951–1953, или «Атлантиды» для 17 инструментов, 1959) и не дает даже отдаленного представления о том, какую конфигурацию принимают происходящие в этой музыке события. Приходится принять на веру утверждение автора, что для правильного заполнения этой абстрактной, не слишком информативной матрицы требуются «исследовательское терпение и приложение всех творческих способностей» [19, 41], а его оговорка относительно не вполне детерминиро­ванного характера матрицы, допускающего свободу композиторской воли [19, 41], дополнительно подтверждает сомнения в том, что на основе математических расчетов может быть создано эстетически привлекательное музыкальное целое.

Но непосредственное знакомство с яр­кой, живой, полной «драйва» музыкой «Achor­rip­sis» способно рассеять любые сомне­ния. Вряд ли кому-либо дано оценить, даже при многократном прослушивании, соблюдается ли здесь хотя бы приблизительно пуассоновское соотношение 1 : 4 : 19 : 65 : 107; к тому же сопоставление партитуры с матрицей показывает, что композитор, действительно, местами трактует ее достаточно вольно. Зато здесь неукоснительно соблюдаются законы № 1, 2 и 3. Каждый из трех параметров флуктуирует с нерегулярной, но, несомненно, каким-то образом (похоже, отнюдь не «по-пуас­соновски») упорядоченной частотой, и графическое представление флуктуаций могло бы дать картину, способную до какой-то сте­­пени «удовлетворить интеллектуальные и эс­тетические запросы». Один из коммента­то­ров вычертил для «Achorripsis» график колебаний плотности материала, то есть прозрачности с обратным знаком (см. пример 2, где по оси абсцисс отложены сегменты партитуры (28 сегментов по 6,5 тактов в каждом), а по оси ординат — среднее число звуков (или, скорее, атак) в такте; цит. по [12, 260]). В этой картине есть гармоничная в своем ро­де архитектоника, напоминающая силуэт зданий разной высоты на фоне неба (так называемый skyline) и сообщающая об эстетике и о композиционных особенностях «Achorripsis» заведомо больше того, что можно извлечь из созерцания матрицы.

Пример 2

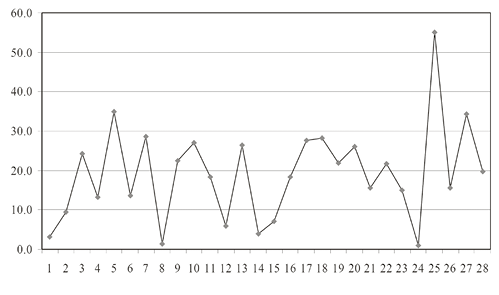
Почти по-веберновски прозрачное начало пьесы (см. пример 3) «намекает» на серийную организацию, но эта иллюзия быстро рассеивается, и дальнейшее представляет собой свободное, артистичное и местами, как обычно у Ксенакиса, агрессивное «разбрасывание звуков». Инструментальные партии изобилуют широкими скачками и нотами в крайних регистрах. Представление композитора об инструментальной виртуозности находит свое особенно характерное воплощение в сжатых мотивах почти неестественно широкого диапазона, наподобие тех, которыми насыщена ткань кульминационного отрезка, совпадающего с единственным четверным событием (такты 156–161, см. пример 4) здесь, в силу закона № 2, достигнута самая высокая для данной партитуры мера интенсивности.

Пример 3

Пример 4

В этом же примере обратим внимание на своеобразную ритмическую полифонию в партиях ударных (ксилофона, вудблока и большого барабана), где нет ни единого совпадения атак по вертикали. Аналогичным образом ударные ведут себя на протяжении всей пьесы. Позднее Ксенакис подверстает под этот свой излюбленный прием чередования атак и пауз (или, точнее, атак и «минус-атак») в неповторяющихся комбинациях математическую теорию решета, смысл которой заключается в «просеивании» множества целых чисел согласно определенным алгоритмам для получения подмножеств с нужными характеристиками. Идеи из этой области алгебры помогают композитору выработать алгоритм получения и комбинирования структурированных наборов длительностей (как в данном случае: «минус-атаки» разной длительности, по всей видимости, распределяются не хаотично, хотя выявить какую-либо регулярность можно разве что при микроскопическом исследовании) или звуковысот (как в ряде более поздних вещей). Такой способ упорядочения дискретных единиц в своих глубинных основах родствен ритмической и звуковысотной модальности; подобно ей, он служит показателем относительно высокого уровня собственно музыкаль­ной значимости/информативности.

Звуковысотные «решёта» — звукоряды с неравномерным распределением отсеянных звуков (по аналогии с «минус-атаками» назовем их «минус-звуками») — утвердились в ряду характерных для музыки Ксенакиса звуковых сущностей с середины шестиде­ся­тых4. Идея конструирования звукорядов по прин­ципу решета возникла под влиянием изучения «вневременны́х» структур античной и византийской музыки, включая тетра­хорды, системы/шкалы и модусы/ихосы (гласы), и метабол — осуществляемых во времени переходов между структурами. По мнению Ксенакиса, вытеснение этих структур «приглаженными» григорианскими тонами, на основе которых сформировалась мажоро-минорная тональность, придающая чрезмерное значение временнóму фактору, бесконечно обеднило музыку, и одну из своих задач он видел в возрождении вневременны́х структур и метабол, но уже с использованием математических методов. Свое изложение методов «просеивания» единиц, получения «решёт» и организации переходов (метабол) Ксенакис, как обычно, снабжает многочислен­ными формулами [18, 180 ff]. Хотя в качестве наглядной иллюстрации он приводит мате­матическую модель мажорной гаммы, его выкладки, по идее, могут в равной мере отно­ситься к любым параметрам звука, исчисляе­мым в дискретных единицах, в том числе к длительности.

Ранний образец «трансфера» теории ре­шета в область звуковысотных отношений — пятнадцатиминутная композиция для вио­лон­чели соло «Nomos alpha» («Первый закон» или «Первый напев/лад», 1966), удостоенная детального, проиллюстрированного рисунками и схемами, авторского разбора [18, 219–236]. Неудивительно, что она оказалась особенно привлекательной для аналитиков (чему вдобавок способствовала относительная простота нотации для струнного инструмента соло)5. Когда один из них, обнаружив в нотном тексте ряд структурных решений, проблематичных с точки зрения теории, обратил на это внимание автора, тот ответил: 

<…> (а) в пылу работы мой карандаш может выйти из-под контроля, и я обнаруживаю это слишком поздно, уже после публикации; (б) иногда я меняю некоторые детали, чтобы сделать их интереснее для слуха; (в) я допускаю теоретические ошибки, ведущие к ошибкам в деталях [композиции]. Я по возможности стараюсь быть последовательным в том, что я сочиняю, но это мне не всегда удается <…> Полагаю, что отношение между теорией и ее реализацией иногда может не быть взаимно однозначным [14, 44]6.

Следовательно, мы имеем основания в очередной раз отвлечься от авторского тео­ретического антуража и обратить внима­ние на те особенности «Nomos alpha», которые делают эту пьесу «интересной для слуха». Прежде всего это широкое использование нестандартных приемов игры — таких, как четвертитоны, тройные ноты (в том числе узкоинтервальные кластеры), длинные и короткие glissandi квартовыми флажолетами и двойными нотами, быстрые удары col legno, биения, скордатуры нижней струны (обяза­тельно жильной) вплоть до C ₁ и тому подоб­ное, — и крайне малое число нот, взятых pizzicato или arco обычными штрихами, без изменений натурального тембра инструмен­та, в темперированном строе. «Nomos alpha» ассоциируется не столько с алгоритмически сгенерированными вневременны́ми структурами и законосообразными переходами (метаболами), сколько со спонтанным «разбрасыванием» контрастных звуковых сущностей вдоль временнóй оси; этот масштабный этюд новой трансцендентной виртуозности легко представить также как инструменталь­ную драму со множеством колоритных, экстравагантных персонажей. На ассоциации со звукорядами-решётами настраивает главным образом феноменально сложный пассаж из двух вначале полиритмически расходящихся, а затем движущихся параллельно гамм, помещенный в конце пьесы (см. пример 5): в структуре каждой из гамм угадывается неоктавное решето с непериодическим распределением пропущенных ступеней («минус-звуков»). Поскольку в произведении для струнного инструмента параметр прозрачности в принципе не может подвергаться слишком широким флуктуациям, «Nomos alpha» предстает своеобразной иллюстрацией сформулированного выше закона № 3, постулирующего параллельный рост интенсивности и информативности; кульминация по обоим параметрам достигается перед самым концом пьесы в полном соответствии с традициями виртуозного инструментализма.

Пример 5

***

В конце пятидесятых арсенал Ксенакиса обо­га­тился теорией особого рода вероят­ностных процессов, которые в честь их первого исследователя принято называть марковскими. Особенность таких процессов заключается в том, что будущее не зависит от прошедшего, но его можно статистически предсказать исходя из настоящего; о марковском процессе принято говорить, что он «не помнит» прошедшего. Частный случай марковских процессов — марковские цепи, состоящие из дискретных событий; вероятность собы­тия, следующего за известным событием n, может быть вычислена на основании характеристик n и не зависит от того, что ему предшествовало. Ясно, что музыкальные формы более или менее привычных типов, описываемые формулой i : m : t, не обладают марковскими свойствами, ибо m непременно содержит память об i, а t — об обеих предшествующих фазах развития. Но нечто «марковское», несомненно, присутствует в экстравагантном отрывке из медленной части Шестой («Простой») симфонии Карла Нильсена (1926), показанном в примере 6. Линия вторых скрипок здесь — гипертрофированное m, «забывшее» об i и блуждающее в поисках t, — один из самых откровенно «стохастических» моментов во всей музыке до Ксенакиса. Вначале (сразу после цифры 1) дано упорядоченное множество из семи единиц (хроматический звукоряд от h¹ до f² ), а затем оно многократно рекомбинируется случайным образом, всякий раз оборачиваясь новыми последованиями. Думается, Ксенакис мог бы привести этот пример в качестве простой общепонятной иллюстрации самого общего принципа, лежащего в основе «марковской стохастической музыки».

Пример 6

В своем трактате Ксенакис подробно излагает ее теорию и практику, подкрепляя изложение солидным логико-математическим аппаратом, графиками и чертежами [19, 61–131]. Исходная позиция его теории заключается в том, что всякий звук, по аналогии с атомом, представляет собой объединение элементарных частиц или квантов, имеющих тройственную природу: длительность, частоту (высоту) и интенсивность (громкость). Исключая из рассмотрения длительность, Ксенакис трактует «атомарный» звук как объединение высоты и громкости. Массы («облака») таких «атомов» размещаются в «сетках», где по вертикали откладываются значения громкости, а по горизонтали — значения высоты. Сетка с атомарными звуками, распределенными внутри нее с варьируемой плотностью, заполняет собой некоторый (не определенный точно, но короткий) промежуток времени; несколько сеток могут складываться в «тетрадь», отражающую процесс развития сложного звука, полученного из множества атомарных частиц. Переход от сетки к сетке организуется по принципу марковского процесса: значения параметров в каждой очередной сетке вычисляются на основании данных той сетки, которая ей предшествует.

Переходя к практическому приложению теоретических выкладок, Ксенакис замечает, что «вычисления a priori не гарантируют полученный таким образом звуковой результат; принимая решения и анализируя их, следует руководствоваться интуицией и опытом» [19, 98]. В качестве основного образца практического приложения теории приводится не слишком значительная партитура «Analogique A» для струнных (1958), где россыпи атомарных звуков сливаются в слабо дифференцированную, почти монотонную массу (следствие закона № 1), и лишь попутно упоминается основанный на той же математической структуре, но несравненно более богатый по музыкальному материалу «Syrmos» для 18 струнных (1959), при сочинении которого интуиция и опыт явно сыграли более существенную роль. Заглавие пьесы переводится с греческого как «тяга», «вытягивание»; по-новогречески συρμός означает также «поезд» (близкая аналогия этому слову во всем многообразии его значений — немецкое Zug). В примечании к соответствующему месту трактата Ксенакис перечисляет базовые «звуковые сущности» пьесы: (1) сети параллельных горизонтальных линий; (2) се­ти па­раллельных восходящих glissandi; (3) се­ти параллельных нисходящих glissandi; (4) се­ти параллельных перекрещивающихся (восхо­дя­щих и нисходящих) линий; (5) облака pizzi­cati; (6) атмосферы, создаваемые ударами древком смычка (col legno) и короткими glissan­di col legno; (7) геометрические конфигурации сходящихся или расходящихся glissan­di; (8) конфигурации glissandi, трактуемые как ров­ные скошенные поверхности [19, 98]. Уже из этого перечисления следует, что наряду с атомарными звуками (отдельными pizzi­cati и ударами col legno) и их конгломератами (облаками, «атмосферами») в «Syr­mos» фигурируют и сложные звуки (горизонтали, glissandi и их комплексы — «сети»), наделенные заведомо более высоким формообра­зующим потенциалом. То, что отношения между этими фактурными типами организу­ются именно по принципу марковской цепи, приходится принять на веру; так или иначе, характеристика «Syrmos» как цепочки («цу­га») событий или сущностей, извлекаемых («вытягиваемых») друг из друга согласно прихотливой, но, по-видимому, достаточно органичной логике, вполне адекватна ее идее и форме. Добавим, что на протяжении всей двенадцатиминутной пьесы поддерживается чрезвычайно высокий уровень общей ин­тенсивности («драйва»), что делает «Syrmos» одной из самых эффектных, выигрышных, «информативных» (в оговоренном выше смысле) партитур Ксенакиса (следствие закона № 3).

Следующей теорией, привлеченной Ксенакисом для обоснования своих музыкальных идей, стала символическая логика. В ее основе — операции конъюнкции (a 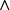b — «и a, и b»), дизъюнкции (a 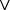b — «или a, или b») и отрицания (a ¬ b — «a не b»), осуществляемые с элементами неких множеств. В трактате «Формализованная музыка» возможности применения этих операций к параметрам музыкального звука — все к тем же высоте, длительности и громкости — обсуждаются весьма детально и, как обычно у Ксенакиса, с формулами, рисунками и схемами [19, 185–208]. В 1964 году из-под его пера вышел масштабный опыт в области стохастики и символической логики, увлекательный в художественном отношении и более чем спорный с точки зрения методологии: «Eonta» для фор­тепиано, двух труб и трех тромбонов. Эта партитура длится 18–20 минут (481 такт на ²/₂ ) и по продолжительности превосходит любое из написанных ранее произведе­ний Ксенакиса. Вынесенное в заглавие древ­не­гре­ческое слово буквально значит «сущие», то есть почти синонимично важному для Ксе­­накиса термину «сущности» (êtres). Трудно сказать, имел ли Ксенакис в виду «звуковые сущности» (êtres sonores), упомянутые в его трактате (который ко времени появления «Eonta» уже вышел в свет, поэтому этот опус там не комментируется); согласно авторскому предуведомлению к партитуре, произведение «названо так в честь [фило­софа-досократика] Парменида», но связь кон­цепции «Eonta» с философией Парменида неясна7. Множество неясностей возникает также в связи с использованием в партитуре «Eonta» аппарата символической логики. Объектами операций конъюнкции, дизъюнкции, отрицания и тому подобного выступают множества звуков темперированной шкалы. Всего множеств три: полное (вся клавиатура) и два частичных. По ходу партитуры в качестве ориентиров выставлены буквенные обозначения множеств (соответственно Σ, Θ и Ψ, поодиночке или в разных сочетаниях) и условные знаки, указывающие на то, каким логическим операциям они подвергнуты. Поскольку автор не дает никаких разъяснений относительно звуковысотного состава частичных множеств, аналитики вынуждены опираться на буквенные обозначения; анализ со всей определенностью показывает, что при совершении логических процедур композитором был допущен ряд ошибок, причем многие из них видны буквально невооруженным глазом (например, в составе множества – Θ, отрицающего множество Θ, могут встречаться звуки, фигурирующие в Θ, и тому подобное).

Ясно, что неаккуратность при осуществ­лении предкомпозиционных расчетов ни­чуть не дискредитирует Ксенакиса как ху­дож­ника. В математических ошибках Ксена­киса нетрудно усмотреть своего рода эквивалент пресловутых оговорок по Фрейду: как бы ученый интеллектуал ни старался дисциплинировать собственное «эго», он не в силах укротить иррациональную природу глубинных творческих импульсов. Соответственно, у нас есть основания усматривать в физико-математическом антураже творчества Ксенакиса не столько конкретную методо­логию композиторской работы, сколько ис­точник интересных метафор, позволяющих взглянуть на музыку с неожиданной стороны и расширяющих поле ее возможных толкований. Одна из таких метафор — осуществленный нами выше опыт трансфера «газовых» законов в сферу организации звукового материала8; не исключено, что она может иметь смысл в применении к разной музыке, но натолкнуть на нее способна прежде всего музыка Ксенакиса, оперирующая большими звуковыми массами — «облаками» и «атмо­сферами», — о которых естественнее всего рассуждать в таких категориях, как масса, плотность, давление, объем и кинетическая активность.

***

В пятнадцатиминутной композиции «Syna­phaï» для фортепиано и оркестра (1969) Ксенакис продолжает испытывать формообра­зую­щие идеи натурфилософского происхож­дения. Одна из них — «арборесценция» [13, 89–98]9 (от латинского arbor — «дерево»), то есть древовидное разветвление. Арборесценции многочисленны в живой и неживой природе (кроны и корни деревьев, речные системы, системы кровеносных сосудов, отростки нервных клеток и так далее). В применении к музыке под арборесценцией может иметься в виду последовательное добавление к некоей линии (или извлечение из нее) производных линий, разворачиваемых в стороне от исходной, но сохраняющих связь как с ней, так и между собой. Фольклорная гетерофония, наращивание полифонической ткани на cantus firmus, микрополифония — не что иное, как разновидности арборесценции. Во всех подобных случаях на передний план выходит действие закона № 1, регули­рую­щего отношение между инфор­ма­тив­но­стью и прозрачностью при срав­ни­тельно неизменном (ввиду сходства «арборесци­рую­щих» линий) уровне интенсивности. В от­личие от полифонии привычного типа, обеспечи­вающей ясную прослушиваемость всех линий (и, подобно контрапункту событий в «Achor­ripsis», подпадающей скорее под действие закона № 2: интенсивность непрерывно флуктуирует, и ее максимум при­хо­дится на стретты), здесь общая картина затуманивается, контуры размываются, структурная определенность вытесняется «стохастикой».

В начале «Synaphaï» на cantus firmus в виде тянущегося dis¹ фортепиано, окруженного облаком струнных, почти сразу наслаиваются восемь линий, причем для каждой из них предусмотрен собственный нотоно­сец (местами число нотоносцев в партии фортепиано доходит до одиннадцати, превышая число пальцев у пианиста). Нижние два нотоносца помечены ремаркой «резко», остальные семь — «текуче» (см. пример 7, партии струнных опущены). На протяжении большей части пьесы у фортепиано преобладает артикуляция второго типа — legatissimo, quasi glissando; она вытесняется «резким» типом артикуляции только в последней трети партитуры. Примерно таково же соотношение звуковых сущностей в оркестре.

Пример 7

Слово συναφαὶ буквально переводится как «контакты» или «соприкосновения» и по смыслу родственно «токкате»; воз­можно, в намерения автора входила ассоциация с «ток­катным» аспектом пьесы — мно­жест­вен­ными прикосновениями пальцев к клавишам в репетициях. Согласно вступительному тексту к партитуре, заглавие указывает на «соединение двух звуковых миров — разных, но взаимодополняющих», и на «ис­сле­дуемые здесь проблемы близости, свя­зи, воздействия, зависимости» [8]. Очевид­но, речь идет о природе соприкосновений между фортепиано и оркестром: пока у фортепиано преобладает «текучая» артикуляция, оркестровая ткань «окутывает» фортепианную партию, фортепианные фигурации «ар­бо­рес­цируют» в оркестре. С выходом на первый план «резкой» артикуляции отношения меж­ду звуковыми мирами становятся более конф­ликтными (пользуясь терминоло­гией, применяемой к другим произведениям Ксе­­накиса, «конъюнкции» уступают место «дизъ­юнк­циям»). Восприятию «Synaphaï» как композиции из двух контрастных разделов дополнительно способствует наличие двух каденций: «текучей» в первой половине и «резкой» во второй, близ точки золотого сечения.

Ниже, в чисто оркестровом фрагменте перед самым концом пьесы, устанавливается равномерно высокий уровень непрозрачности, что могло бы привести к монотонному информационному шуму, если бы не мелкие флуктуации интенсивности внутри массивного оркестрового tutti (закон № 3). На последней странице фортепиано возвращается к «текучему» типу изложения и, так сказать, де-арборесцирует к нижнему пределу клавиатуры в контрапункте с трио не звучавших до этого момента томтомов (см. пример 8). Партитуру завершает их продолжительное тремоло — внезапный «вброс» новой инфор­мации на фоне быстрого восстановле­ния исходной фактуры: эффективный дра­ма­тур­ги­ческий прием, реализующий центро­­бежно-центростремительный архетип в не­сколь­ко усложненном по сравнению с «Me­ta­sta­sis» варианте, предполагающем не толь­ко взаимное «соприкосновение» конца и начала, но и заметное качественное об­новление.

Пример 8

В связи с возможной натурфилософской подоплекой «Synaphaï» стоит напомнить, что синапсами в физиологии называют точки соприкосновения между двумя нервными клетками. Среди последних есть центростре­мительные (сенсорные) и центробежные (двигательные). Проходя вдоль сенсорного нейрона, нервный импульс достигает синапса на конце одной из ветвей его арборесцирующего отростка (аксона), оттуда передается на «принимающий» отросток (дендрит) следующего нейрона и тому подобное. Находя нужные синапсы, импульс достигает центральной нервной системы; там он преобразуется в ответный импульс и вновь через ряд синапсов, соединяющих аксоны с дендритами, возвращается на периферию, вызывая соответствующую двигательную реакцию. Весь этот комплекс разнонаправленных процессов именуется рефлекторной дугой, а прохождение через каждый новый синапс можно представить как очередной этап вероятностного (марковского) процесса. Метафора синаптической передачи нервных импульсов по рефлекторной дуге идеально согласуется с заглавием пьесы и, на наш взгляд, отнюдь не противоречит комплексу ее композиционных особенностей — с поправкой на то, что движение импульса по дуге занимает доли секунды, тогда как в «Synaphaï» оно развернуто в достаточно масштабную драму.

***

Можно было бы привести и другие примеры, указывающие на то, что источником «сюжетов» для инструментальных драм Ксенакиса служит не столько строгая и точная современная научная мысль, сколько давно уже не актуальная для позитивных наук натурфилософия, то есть набор самых общих умозрительных представлений о макро- и мик­ромире, о физических законах и природных процессах. Это отчасти подтверждается высказываниями самого Ксенакиса, любившего обосновывать свои идеи не только данными современных точных наук — во многих случаях трактуя их произвольно, мифологизируя и даже, возможно, до некоторой степе­ни мистифицируя их, — но и ссылками на досократиков, стоиков, эпикурейцев, Платона, Аристоксена и Евклида. Угадывае­мый в произведениях Ксенакиса элемент драмы, разыгрываемой с участием природных сил, неоднократно вдохновлял хореографов. Так, Джордж Баланчин поставил балеты на му­зыку «Metastasis» и «Pithoprakta», а в 1971 году Ксенакис по заказу Баланчина сочинил одноактный балет «Antikhthon» («Анти-Земля») для большого оркестра. Название отсылает к пифагорейской концепции «другой», невидимой земли, которую Ксенакис связывал с современными научными концепциями ан­ти­материи и параллельных вселенных; загадочные коннота­ции заглавия, по мысли Ксе­накиса, должны были стать для хореогра­фа неким эквивалентом сюжетной канвы [15, III]. На размышления наталкивают такие названия его партитур для большого оркестра, как «Jonchaies» (франц. «Тростниковые заросли», 1977) или «Lichens» (англ. «Лишайники», 1983); соответствующие образы могли привлечь ком­позитора постольку, поскольку за ни­ми встают много­слойные, обильно арборесцирующие, не осо­бенно структурированные и вместе с тем каким-то стихийным образом упорядоченные множества. Аллюзия на зрелищную иг­ру природных явлений содержится в загадочном эпиграфе к парти­туре «Cendrées» (франц. «Пепельные») для смешанного хора (без слов) и оркестра (1973): «Перед началом осени, перед началом лета, перед началом любого времени года, когда небо мягко как пух, когда оно опускается и встречается с землей, все становится мо­лочно-бе­лым тогда; и это длится долго порой. Это не туманы, не росы, а пепельность» [17, I, II]10.

В связи с идеей «Metastasis» Ксенакис упомянул и такой источник трансфера, как юношеское впечатление от разгона политической демонстрации, когда мощное упорядоченное движение мгновенно превратилось в хаотическую массу [13, 52]. Очевидно, поведение массы людей также может трактоваться натурфилософски, как природный процесс, регулируемый соответствующими законами. Если мы попытаемся сформулировать их, взяв за основу наиболее очевидные параметры, характеризующие толпу, — численность (обозначим ее литерой Q), однородность (U) и организованность (O), — то мы получим еще одну триаду знакомого нам типа. Изобразим ее в виде простейших общепонятных формул:

1. Q = const, U ~ O

2. U = const, O ~ Q–¹

3. O = const, Q ~ U–¹

Позволим себе предположить, что какие бы звуковые сущности ни выступали персонажами всех этих драм и какие бы научные концепции и представления — будь то распределение Пуассона, теория решета, символическая логика, марковские цепи, арборесценции, клеточные автоматы (в некоторых поздних партитурах), объективные законы поведения толпы и тому подобное — ни привлекались в качестве источников трансфера, глубинная структура11 музыки Ксенакиса, как правило, восходит к триаде универсальных законов, описывающих соотношения между параметрами массовых явлений.

Литература

1. Акопян Л. Анализ глубинной структуры му­зыкаль­ного текста. М. : Практика, 1995. 255 с.
2. Вайль П. Стихи про меня. М. : Астрель: CORPUS, 2011. 671 с.
3. Ксенакис Я. Формализованная музыка. Новые формальные принципы музыкальной композиции. СПб. : Санкт-Петербургская гос. консерватория, 2008. 123 с.
4. Bayer F. De Schönberg à Cage. Essai sur la notion d’espace sonore dans la musique contemporaine. Paris : Klincksieck, 1981. 217 p.
5. Childs E. Achorripsis: a Sonification of Probabili­ty Distributions // Proceedings of the 2002 Inter­na­tional Conference on Auditory Display. Kyo­to, Japan, July 2–5, 2002. URL: http:// icad.org/websiteV2.0/Conferences/ICAD2002/proceedings/16_EdwardChilds.pdf (дата обращения: 15.10.2020).
6. Chrissochoidis I., Mitsakis C., Houliaras S. Set theory in Xenakis’ EONTA // International symposium Iannis Xenakis / ed. by A. Georgaki and M. Solomos. Athens : The National and Kapodistrian University, 2005. P. 241–249.
7. Exarchos D., Jones D. Sieve analysis and construction: Theory and implementation // Proceedings of the Xenakis International Symposium. Southbank Centre, London, 1–3 April 2011. URL: https://research.gold.ac.uk/15753/1/11.2-Dimitris-Exarchos-%26-Daniel-Jones.pdf (дата обращения: 15.10.2020).
8. Fleuret M. Notes sur Synaphaï // Xenakis I. Synaphaï. Paris : Salabert 17395, 1985. P. II.
9. Jones E. An Experiential Account of Musical Form in Xenakis’s String Quartets // Intimate Voices. The Twentieth-Century String Quartet. Vol. 2: Shostakovich to the Avant-garde / ed. by E. Jones. Rochester : University of Rochester Press, 2009. P. 138–161.
10. Schaeffer P. Traité des objets musicaux. Paris : Seuil, 1966. 671 p.
11. Solomos M. Iannis Xenakis. Trois composantes de l’univers xenakien // Théories de la composi­tion musicale au XXe siècle / sous la direction scientifique de N. Donin et L. Feneyrou. Vol. 2. Lyon : Symétrie, 2013. P. 1057–1080. (Symétrie recherche, série 20–21.)
12. Squibbs R. The Composer’s Flair: Achorripsis as Mu­sic // International symposium Iannis Xenakis / ed. by A. Georgaki and M. Solomos. Athens : The National and Kapodistrian University, 2005. P. 258–264.
13. Varga B. A. Conversations with Iannis Xenakis. Lon­don : Faber & Faber, 1996. 255 p.
14. Vriend J. Nomos alpha. Analysis and Comments // Interface. No. 10 (1981). P. 15–82.
15. Xenakis I. Antikhthon. Paris : Salabert 17038, 1986. IV, 63 p.
16. Xenakis I. Arts/Sciences. Alliages. Tournai : Caster­man, 1979. 151 p.
17. Xenakis I. Cendrées. Paris : Salabert 17187, 1974. II, 65 p.
18. Xenakis I. Formalized Music. Thought and Mathe­matics in Composition. Revised edition. Stuyvesant, NY : Pendragon Press, 1992. 387 p.
19. Xenakis I. Musiques formelles: nouveaux principes formels de composition musicale. Paris : Richard-Masse, 1963. 232 p.