Использование современных компьютерных методов для исследования фонограмм традиционной музыки позволяет вычислить точную мелодическую линию и далее определить звуковысотную систему, применяемую исполнителем. Предложенная автором методика анализа звукоряда [6] основана на предположении, что слушатель опознает ступени звукоряда по их большему суммарному времени звучания в процессе исполнения; промежуточные же высоты, звучавшие меньшее время, не фиксируются слухом как ступени. Для оценки относительного времени звучания на разных высотах производится статистический анализ звуковысотного рисунка; ступени звукоряда определяются по положениям локальных максимумов статистического распределения времени звучания высот. Все необходимые вычисления реализованы автором в компьютерной программе SPAX1.

Экспериментальное исследование звукоряда производится обычно в ситуации, когда его структура и параметры заранее неизвестны и их предстоит определить на основе измерений. На точность результата влияют наличие проходных высот и мелизматики, возможные погрешности исполнения, а также ограниченная точность методов анализа высоты звука. Последующая проверка результатов компьютерного исследования затруднена тем, что музыковеды «европейской» школы не определяют на слух интервалы уровня 20..40 центов, хотя могут отметить наличие этих отклонений высоты от привычных им ступеней 12-полутонового равномерно-темперированного строя. В связи с этим мелодии традиционных музыкальных культур при слуховой расшифровке часто фиксируются музыковедами академической школы с помощью именно 12-полутонового строя [12]; погрешности по высоте и по длительности звуков, возникающие при таком представлении, анализировались в работах автора [7; 8].

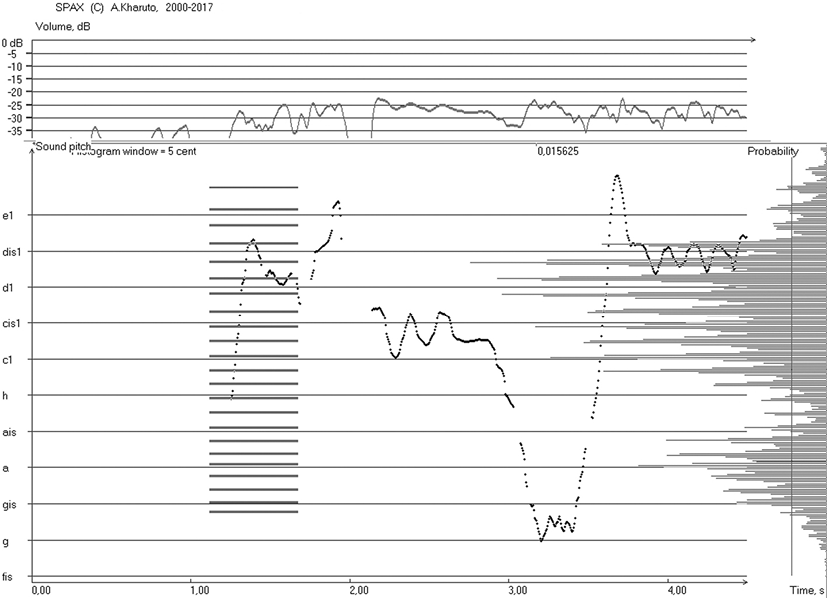
В рассматриваемой методике компьютерного анализа сначала вычисляется звуковысотный рисунок фонограммы с малым шагом по времени Δt (обычно Δt = 5..10 мс); пример графического представления результата звуковысотной расшифровки (мелограмма) приведен на рис. 1. На мелограмме верхний график показывает текущую интенсивность звука, а нижний — звуковысотный рисунок (горизонтальная ось — время в секундах; вертикальная — высота звуков, эта ось размечена в соответствии с 12-полутоновым равномерно-темперированным строем). В правой части показан график экспериментально полученного ста­тистического распределения (гистограмма) времени пребывания звука на разных высотах (ось вероятности направлена справа налево). Вертикальная линия справа показывает пороговый уровень отбора ступеней. Толстые линии левее соответствуют положениям выявленных программой ступеней звукоряда.

Рис. 1

Для экспериментального построения ста­тистического распределения исполь­зуемый диапазон высот разделяется на «окна» равной ширины. В программе SPAX эта ширина равна 5 центам, что соответствует возможной погрешности определения высоты при компьютерном анализе [9]. При построе­нии гистограммы подсчитывается суммарное время пребывания высоты ti в каждом i–м «окне». Далее для выявления ступеней задается относительный порог отбора θ по суммарному времени звучания; высота фиксируется как ступень, если

ti ≥ Tmax × θ, (1)

то есть время звучания ti составляет не менее Tmax × θ, где Tmax — длительность звучания «основной» по длительности (самой «долгой») ступени; порог выбирается в пределах 0 < θ ≤ 1.

На графике гистограммы высот ступеням звукоряда соответствуют «пики» распределения, пересекающие линию порога справа налево (см. «Probability» на рис. 1). В данном примере основная по длительности использования ступень — это dis1 минус 30 центов (то есть на 30 центов ниже dis1); время ее звучания — Tmax= 3,16 c. Показанная на рис. 1 линия порога соответствует уровню θ = 0,1.

В процессе анализа по такому алгоритму часто обнаруживаются ступени, расположенные «слишком близко» — «варианты» исполнения одной и той же подразумеваемой ступени звукоряда. С целью выявления только «истинных» ступеней при анализе две соседние предполагаемые «ступени» объединяются и заменяются одной, если интервал между ними меньше заданного исследователем значения Qmin. При этом учитывается время звучания на каждой из высот: «усредненная» ступень сдвигается к высоте, звучавшей дольше [6; 9].

Очевидно, что при максимально высоком уровне порога (θ = 1) будет зафиксирована только одна ступень, звучавшая (в сумме) дольше всех. Далее при понижении порога алгоритм будет выделять и другие ступени звукоряда, число которых в целом увеличивается с уменьшением θ, поскольку все большее число возможных ступеней удовлетворяет условию (1). При малых значениях θ возможна ошибочная фиксация «ступеней» в точках «пиков» гистограммы, случайно возникших в результате наложения мелизматики, погрешностей исполнения и проходных высот между звуками. При этом в ходе исследования возникает вопрос: каким надо выбрать порог θ, чтобы обнаружить высоты всех «истинных» ступеней?

Нижнее ограничение для величины θ задает слуховое восприятие человека. Известно, что возможность слухового определения высоты звука связана с его длительностью, а именно, время, необходимое для распознавания низких звуков, оказывается заметно бóльшим, чем для высоких звуков. На основании ряда опубликованных данных [1; 3] можно видеть, что на интервале высот примерно от C (65,4 Гц) до a3(1320 Гц) это время убывает пропорционально час­тоте основного тона от 75 мс до 12 мс, но при дальнейшем повышении частоты звука немного увеличивается (до 15..18 мс). Таким образом, тоны, звучавшие менее 12 мс, нет смысла учитывать при определении звукоряда, поскольку они не будут распознаны по высоте среднестатистическим слушателем.

В рассматриваемом примере суммарное время звучания самой «долгой» ступени составляет Tmax= 3,16 c; значение θ = 0,1 соответствует суммарной длительности зву­чания тона 316 мс, то есть примерно длительности 3/16 при темпе 120 ударов в минуту. Величина порога θ = 0,01 соответствует отбору ступеней, прозвучавших в сумме не менее 3,16:100 = 31,6 мс (почти точно 1/64). Все указанные значения заметно превышают минимальную длительность в 12 мс. (Напомним, что при этом темпе длительность целой ноты составляет 2 с, половинной — 1 с, четверти — 0,5 с, 1/8 – 250 мс, 1/16 – 125 мс и так далее.)

Выбор минимально допустимого интер­вала между ступенями Qmin также влияет на результат, поскольку все интервалы менее этой величины оказываются «запрещенными». При выборе ограничения Qminследует учесть, что величина слуховой звуковысотной чувствительности составляет в разных диапазонах от 5 до 10 центов [1], то есть ступени звукоряда не могут располагаться ближе Qmin ≈ 10..15 центов — иначе они просто не будут различаться слушателем. По-видимому, анализ целесообразно начинать с этих малых значений Qmin. В пользу малых величин Qmin свидетельствует и то, что ранее в наших исследованиях русского народного пения [10; 11] было выявлено использование числа ступеней в октаве от 15 до 30 и более. Это соответствует интервалам между ступенями примерно от 30..40 до 70..80 центов. Ряд последующих работ, касающихся анализа звукорядов традиционных культур Азии [4; 5; 13; 14], показал, что музыканты этого региона час­то используют интервалы около 25 центов.

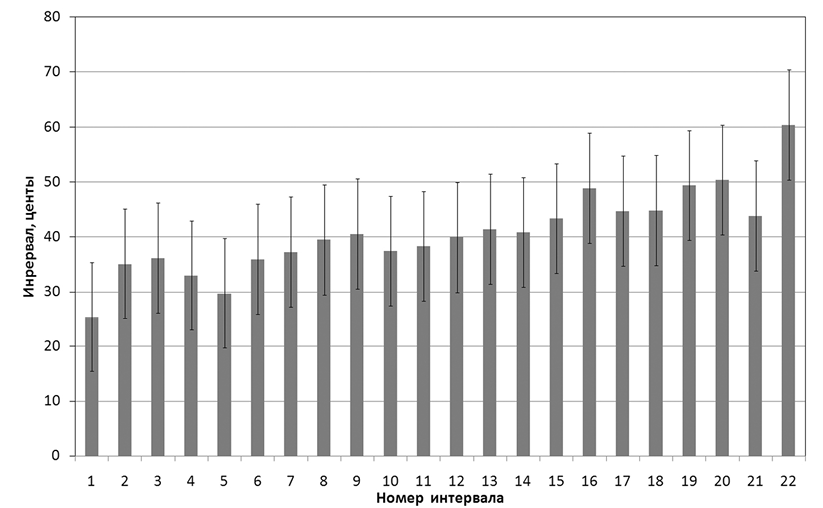
В соответствии с описанной ранее методикой [6; 9] пробное выявление ступеней проводилось при разных сочетаниях параметров анализа θ и Qmin; далее по результатам анализа отыскивались «зоны стабильности» (см. об этом [6]), в пределах которых при постоянном пороге θ изменения минимального интервала Qmin не сказываются на числе обнаруженных ступеней N, то есть величина Qminоказывается меньше, чем средний интервал. Для примера, представленного на рис. 1, при параметрах Qmin = 15..20 центам и θ = 0,1 обнаруживаются N = 23 ступени и получается последовательность из 22 интервалов, графически показанная на рис. 2. Вертикальные тонкие линии с засечками отображают возможную погрешность измерения интервала (± 10 центов, то есть вдвое больше, чем погрешность ± 5центов при измерении каждой высоты).

Рис. 2

Можно ли удовлетвориться этим результатом — или следует повысить порог до значений 0,2 или 0,3 и получить звукоряд с меньшим числом ступеней, зато звучавших дольше, чем в первом случае (и считать эту новую оценку более надежной)? Или наобо­рот, следует понизить порог и охватить бóльшее число возможных ступеней?

На рис. 2 показано, что величины интервалов случайно колеблются около некоторого среднего значения с небольшим разбросом. Рассмотрим возможности при­ме­нения для анализа математической модели звукоряда как системы, в которой сис­те­мо­образующим фактором являются равные интервалы между ступенями (равномерно- темперированный звукоряд). Основ­ным па­ра­метром звуковысотной системы при этом становится единая величина интервала между ступенями, в то время как нижняя и верхняя границы диапазона, охватываемого звукорядом, и число выявленных ступеней (на котором акцентировалась предыдущая методика) могут рассматриваться как вспомогательные переменные.

Для определения системообразующего интервала вычислим среднюю величину интервала по совокупности измеренных расстояний между ступенями:

= (I1 + I2 + I3 + … + IN-1) / (N – 1), (2)

где Ik обозначают измеренные интервалы между ступенями с номерами k и k + 1, где k = 1, 2, 3, … N – 1; N — число ступеней.

Поскольку измеренные величины интервалов содержат случайные составляющие (за счет мелизматики, погрешностей исполнения и измерения высот), вычисленная средняя величина интервала может содержать статистическую погрешность. Из теории вероятностей известно, что оценка среднего значения, полученная по n экспериментальным данным (в данном случае — по измеренным интервалам) [2, 312–369], имеет нормальное (Гауссово) распределение и статистический разброс относительно «истинного» значения, зависящий от среднеквадратичного разброса исходных данных σ0 и от их числа nследующим образом:

σср= σ0 /√–n. (3)

Разброс величин измеренных интервалов σ0 можно оценить по самим измеренным интервалам Ik (для этого вычисляется среднеквадратичное отклонение величин интервалов от среднего значения ; в данном примере он оказывается равен 7,37 цента). Далее можно вычислить доверительные границы, в которых с вероятностью Pдов лежит величина «истинного» среднего интервала [2, 317]. При вероятности Pдов = 0,95 эти границы вычисляются по формуле

γ = ± (1,96 × σср). (4)

Очевидно, чем меньше окажется расстояние γ между границами, тем точнее будет полученный результат. Из соотношений (3) и (4) видно, что ширина доверительного диапазона тем меньше, чем меньше разброс измеренных величин интервалов и чем большее число данных (измеренных интервалов) используется. Первый из этих параметров зависит от реально существующего разброса интервалов в исполнении (а также возможного разброса результатов при их измерении); второй связан как со свойствами фонограммы, так и с параметрами анализа — относительным порогом θ и минимально допустимым интервалом Qmin. Для примера (см. рис. 1) при доверительной вероятности 0,95 результаты расчетов для разных уровней порога θ от 0,02 до 0,4 и Qmin = 20 центам показаны на рис. 3. Нижний график — расстояние от среднего значения интервала до доверительной границы. Верхние штриховые линии показывают границы доверительного диапазона (± γ) для соответствующих значений среднего интервала .

Рис. 3

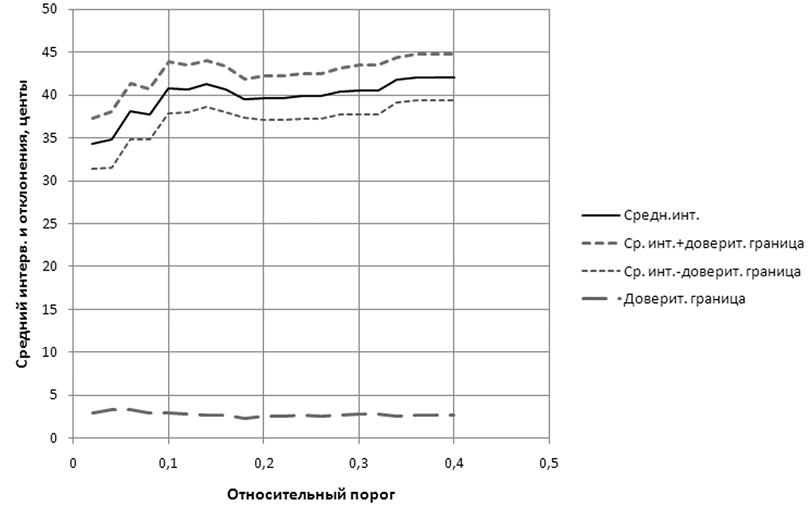
По полученным зависимостям следует выбрать такое значение порога, при котором расстояние от среднего до доверительных границ (γ) минимально либо достаточно мало с точки зрения требований к точности результата. (Исходя из уже упоминавшейся слуховой разрешающей способности «среднего» человека, можно принять в качестве такого требования не более 5..10 центов [1].) Как показывает расчет, в данном случае доверительный диапазон не превышает 3 центов во всей области изменения порога θ от 0,1 до 0,2 при значениях Qmin от 15 до 30 центов. Для выбранной выше величины порога 0,1 (входящей в указанный диапазон) соответствующий звукоряд был показан на рис. 2. Параметром выявленного звукоряда является средний интервал между ступенями, равный 40,8 центам; истинное значение среднего интервала с вероятностью 0,95 лежит в пределах 40,8 ± 2,96 цента.

Отметим, что степень соответствия исследуемого звукоряда предполагаемой здесь модели может быть различной; чем она меньше, тем больше среднеквадратичный разброс величин интервалов и доверительный диапазон (как это происходит в данном примере при увеличении порога до 0,3..0,4 и более). Следует подчеркнуть, что при этом приемлемость величины доверительных границ определяет сам исследователь, исходя из своей задачи и реальных возможностей аппроксимации, иллюстрируемых здесь графиками (см. рис. 3).

Упомянем еще одну проблему, которая появляется при расчете для порога θ, равного примерно 0,15 и выше (см. рис. 3): в этом случае будут обнаруживаться «большие» интервалы — это переходы между поддиапазонами высот, используемыми более интенсивно и образующими на статистическом распределении «холмы» (см. рис. 1). В данном примере выявляются два таких основных поддиапазона, и «большой» интервал формируется примерно между высотами ais и h (однако в других примерах обнаруживается и бóльшее число поддиапазонов, и, соответственно, «больших» интервалов). Включение этих интервалов в формулу (2) для вычисления среднего интервала привело бы к ложному результату, и в программе SPAX они автоматически исключаются из расчета. (Очевидно, в этих местах звукоряд как бы разрывается; задача его возможной реконструкции выходит за рамки данной статьи; частично она рассматривалась в [6].)

По рис. 1 и 2 можно заметить тенденцию к росту измеренных интервалов между ступенями. Для учета этой особенности нужно построить более сложную модель звукоряда. Предполагая рост интервалов примерно постоянным по крутизне (то есть каждый следующий интервал увеличивается на одну и ту же величину по сравнению с предыдущим), можно описать линейную зависимость величины интервала от его номера:

Ik = I1 + μ × (k - 1), (5)

где Ik — интервал между ступенями номер k и (k + 1), μ — шаг увеличения интервала при переходе от k-й ступени к (k + 1)-й, где k = 1, 2, 3, … N – 1.

Применяя для аппроксимации последовательности измеренных интервалов (см. рис. 2) линейную функцию (5) и метод наименьших квадратов, который минимизирует среднеквадратичную погрешность аппроксимации, получаем: I1 = 28,9 центов, μ = 1,03 цента/ступень, то есть приращение интервала составляет около одного цента на каждом переходе к следующей ступени. Как и в предыдущем случае, можно рассчитать доверительные границы параметров модели. Для доверительной вероятности 0,95 величина начального интервала I1 лежит в  пределах 28,9 ± 3,25 цента, а наклон аппроксимирующей линии (крутизна нарастания) находится в пределах 1,033 ± 0,25 центов. Линейное нарастание интервалов иллюстрируется штриховой линией на рис. 4.

Рис. 4

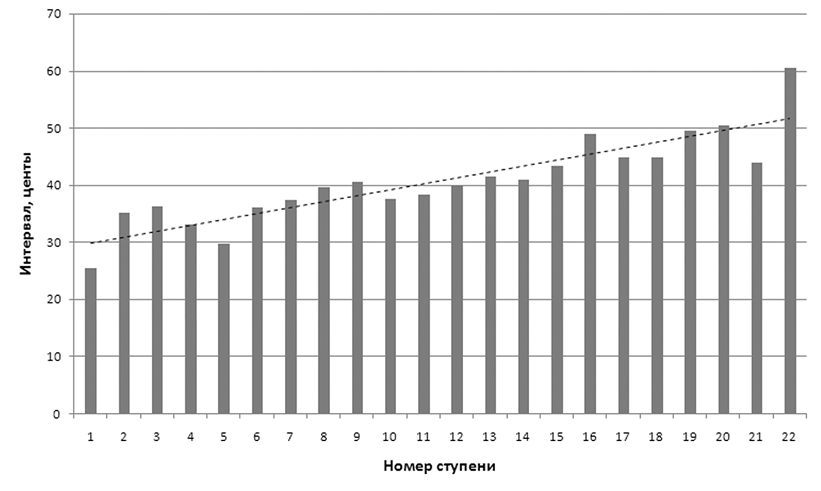
Эта модель точнее описывает зафиксированный звукоряд (стандартное отклонение величин интервалов от средней линии — 3,37 цента), однако весьма малый шаг нарастания интервалов (всего около одногоцента на каждую ступень) не будет заметен на слух (хотя суммарное нарастание интервала более чем на 20 центов нельзя, видимо, игнорировать). Можно еще точнее описать звукоряд, если использовать не линейную, а квадратичную функцию или многочлен с более высокой степенью (или же какие-либо другие аппроксимирующие функции), но это повлечет за собой дальнейшие усложнения модели и увеличение числа ее параметров, что вряд ли оправдано в большинстве задач (однако решение о выборе модели принимает музыковед-исследователь). Таким образом, компьютерные методы дают возможность не только в автоматическом режиме провести точный звуковысотный анализ, но и помогают исследователю в выборе наиболее точного и удобного представления результатов измерений, для которого гарантируется минимум статистической погрешности.

Литература

1. Алдошина И., Приттс Р. Музыкальная акустика. СПб.: Композитор, 2006. 720 с.
2. Вентцель Е. С. Теория вероятностей. 4-е изд. М.: Наука, 1969. 576 с.
3. Кузнецов Л. А. Акустика музыкальных инструментов. Справочник. М.: Легпромиздат, 1989. 368 с.
4. Утегалиева С. И., Харуто А. В. Компьютерное исследование традиционного строя казахской домбры на примере фрагмента из кюя Д. Нурпеисовой «Енбек epi» // Музыковедение. 2013. № 8. С. 28–39.
5. Утегалиева С. И., Харуто А. В. Компьютерные исследования звукорядов казахского кыл-кобыза // Музыковедение. 2013. № 12. С. 38–45.
6. Харуто А. Компьютерный анализ звукоряда по фонограмме // Музыкальная академия. 2010. № 3. С. 83–89.
7. Харуто А. Компьютерный анализ высоты звука в музыковедческом исследовании: информационный аспект // Музыкальная академия. 2016. № 3. С. 98–102.
8. Харуто А. Компьютерный анализ длительно­стей звуков в музыкальном исполнении // Музыкаль­ная академия. 2017. № 3. С. 125–128.
9. Харуто А. Компьютерный анализ звука в музыкальной науке. М.: МГК, 2015. 448 с.
10. Харуто А. В. Компьютерная расшифровка фонограмм фольклорного пения // Творчество в искусстве — искусство творчества / под ред. Л. Дорфмана, К. Мартиндейла, В. Петрова, П. Махотки, Дж. Капчика. М.: Наука; Смысл, 2000. С. 325–336.
11. Харуто А. В., Смирнов Д. В. Использование ком­пьютерного анализа в исследовании звуковысотного строения народной музыки // Музыка устной традиции: материалы между­на­род­ных научных конференций памяти А. В. Руд­­невой / науч. ред. Н. Н. Гилярова. Сост. В. М. Щуров, Н. Н. Гилярова. Науч. труды МГК им. П. И. Чайковского. Сбор­­­ник № 27. М.: МГК им. П. И. Чайковского, 1999. С. 335–340.
12. Gedik, Ali Cenk. Automatic Transcription of Tra­ditional Turkish Art Music Recordings: A Computational Ethnomusicology Approach // A Thesis Submitted to the Graduate School of Engineering and Sciences of İzmir Institute of Technology in Partial Fulfillment of the Re­quirements for the Degree of Doctor Of Philosophy in Electronics and Communication Engineering. January 2012, İZMİR. URL: http://library.iyte.edu.tr/tezler/doktora/elektrik-elektronikmuh/T001006.pdf (дата обращения: 05.08.2019).
13. Iunysova V., Kharuto A. Computer Sound Analysis of Traditional Music of Transcaucasia and Central Asia // 2016 Yearbook for Traditional Music. V. 48. International Council for Traditional Music (UNESCO). P. 136–145. DOI: 10.5921/yeartradmusi.48.2016.0136.
14. Iunysova V., Kharuto A. Computer Sound Analysis of Traditional Music of Asia // Musigi Dunyasi (Baku). 2017. № 1 (70). P. 16–34.