Современные компьютерные технологии позволяют выполнять звуковысотную расшифровку фонограммы, то есть определять частоту основного тона звука в последовательные моменты времени, сохранять эти результаты в памяти компьютера и обрабатывать их. В результате анализа желательно получить нотировку фонограммы, то есть знаковую запись мелодии в какой-либо звуко­высотной системе. В традиционных музыкаль­ных куль­турах встречаются звукоряды с разным числом и расположением ступеней в октаве, и од­ной из актуальных задач музыковедче­ско­го анализа является определение звуко­ря­да исполнителя, на основе которого в даль­нейшем фиксируют мелодический рисунок. Ни лад, ни набор длительностей, используемых в пении или игре на музыкальных инструментах, заранее исследователю не известны.

В ряде статей автора [4; 5; 6; 7; 8; 9] рассматривались разные подходы к анализу звукоряда и системы длительностей в испол­няемой музыке, а также к оценке точности выполненного анализа. В данной работе пред­лагается более общий подход к выбо­ру звукоряда и системы длительностей для нотировки экспериментально полученной фонограммы, базирующийся на оценке точно­сти результата по критерию среднеквадратичной погреш­ности аппроксимации звуковысотного рисунка. Реализация всех необходимых в компьютерном исследовании процедур осуществляется в программе автора SPAX1.

Постановка задачи

Компьютерный анализ фонограммы с целью определения подходящей модели звукоряда начинается с ее звуковысотной расшифровки, то есть с вычисления последовательных значений «мгновенных» высот с достаточно малым шагом по времени — например, через каждые 5 мс. Для одноголосной фонограммы при отсутствии значительных шумов или посторонних тонов удается определить высоту звука с погрешностью не более 4–5 центов [5, 111], что не уступает средней точности различения высоты звука человеком (см., например, [1, 216]). Чтобы получить звуковысотную нотировку фонограммы, то есть определить последовательность тонов постоянной высоты, воспроизводящих мелодический ри­сунок, исследователь выбирает подходящий отображающий звукоряд, содержащий набор ступеней на разных высотах, и составляет последовательность знаков, описывающих порядок появления этих высот (тонов) во вре­мени. Следует отметить, что сама попытка такого знакового отображения мелодии предполагает, что все звуки достаточно точно выдерживаются по высоте на некоторых повторяющихся значениях, соответствующих ступеням звукоряда, а также имеют повторяющиеся или кратные величины длительностей. Для знаковой фиксации необходимо, чтобы при исполнении использовалось конечное число как ступеней звукоряда, так и разных длительностей.

Графически звуковысотный рисунок, полученный при компьютерной расшифровке, может быть представлен как мелограмма — график высоты звука, как показано на рис. 1. В верхнем окне строится график мгновенной интенсивности, в нижнем — мелограмма; высоты и интенсивности откладываются по вертикальным осям слева, время — по горизонтальной. На мелограмму наложена сетка вертикальных линий — меток времени с шагом 0,25 с (что соответствует длительности 1/8 при темпе 120 ударов в минуту).

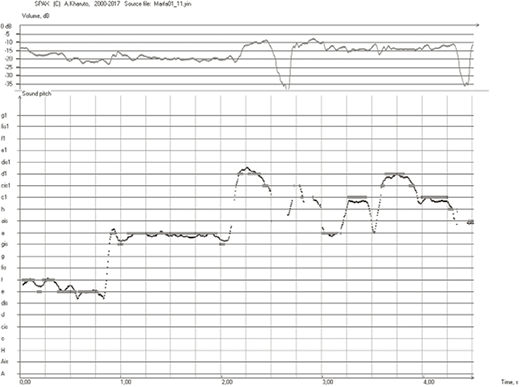
Рис. 1. Пример аппроксимации звуковысотного рисунка (мелограммы) тонами 12-полутонового равномерно-темперированного звукоряда. Исходная фонограмма — фрагмент русского народного пения
Fig. 1. Example of approximation of the pitch line (melogram) with the notes of a twelve-semitone equal temperament scale. The original phonogram is a fragment of Russian folk singing

Для нотировки мелограммы с использо­ва­нием заданного звукоряда построение по­сле­довательности отображающих тонов мо­жет быть выполнено в компьютере путем автоматической замены каждой из «мгновен­ных» высот звуковысотного рисунка ближайшей из высот, соответствующих ступеням звукоряда. Пример такого преобразования (в программе SPAX) для 12-полутонового равномерно-темперированного звукоряда показан на рис. 1. С точки зрения математики при этом исходный звуковысотный рисунок аппроксимируется (то есть приближенно заменяется) кусочно-постоянной функцией — последовательностью постоянных значений высоты на интервалах времени, соответствую­щих тонам. Эта функция отображается на рис. 1 отрезками толстых горизонтальных линий, лежащих на высотах звукоряда.

В примере, отображенном на рис. 1, границы тонов во времени формируются «сами собой»: по мере приближения мелограммы к тому или иному уровню высоты, входящему в звукоряд, аппроксимирующая линия «перескакивает» на соответствующий ближайший уровень. При этом длительности (время пребывания на каждой высоте) могут оказаться довольно произвольными по величине, и их статистика связана с используемым числом ступеней в звукоряде N. Для нотировки долж­на быть выбрана величина минимальной дли­тельности, играющей роль «единицы време­ни» для всех нотируемых звуков, и далее длительность любого тона будет отображена как целое число таких «единиц» [7].

Как известно, любая аппроксимация позволяет представить экспериментальные дан­ные с помощью некоторой математической функции только приближенно, то есть с неко­торой погрешностью. В статье [6] исследова­лись ситуации, когда мелограмма имеет звукоряд с одним шагом (интервалом) между ступенями, а аппроксимация производится с помощью звукоряда с другим шагом. Было показано, что погрешность представления сложным образом зависит от соотношения интервалов в отображающем и исполнитель­ском звукорядах, а также от наличия звуковысотных вариаций и других факторов. В общую погрешность аппроксимации входит также составляющая, обусловленная конечной точ­ностью определения высоты звука путем численного анализа фонограммы [5, 111]. В дан­ной работе предлагается оценивать качество нотировки на основе погрешности аппроксимации звуковысотного рисунка при выбранном отображающем звукоряде и системе фиксации длительностей2.

При выборе типа отображающего звукоряда имеются по крайней мере две возможности. Первая — это равномерно-темперированный ряд с N ступенями в октаве (в частном случае при N = 12 получается «европейский» 12-полутоновый звукоряд, при N = 24 — четвертитоновый звукоряд, и так далее; вообще говоря, может быть выбрано любое целое значение N > 1). Вторая возможность (реализуемая, в частности, в программе SPAX) — это использование собственного звукоряда исполнителя, который может содержать разные интервалы между ступенями (положения ступеней определяются путем статистического исследования мелограммы — см., например, [4]).

Одной из задач данной работы является сопоставление погрешности аппроксимации при применении для нотировки одних и тех же фонограмм обоих типов звукорядов. Априори можно ожидать, что использование собственного звукоряда даст меньшую погрешность, поскольку для его построения используется анализ реальной структуры высот мелограммы, однако равномерно-темперированный звукоряд более понятен и привычен музыковедам европейской школы. Как показано ниже, использование собственного звукоряда исполнителя обеспечивает либо меньшую погрешность нотировки мелограммы по сравнению с использованием равномерно-темперированной аппроксимации, либо требует меньшего числа ступеней звукоряда. Величина выигрыша зависит от характера фонограммы.

Оценка точности аппроксимации высоты и длительности звука

В процессе подбора отображающего (аппрок­симирующего) звукоряда качество аппрок­симации оценивается по степени совпадения его ступеней с мгновенными высотами в звуковысотном рисунке. Для оценки каче­ства в каждый момент времени t следует оценить разницу ε (t) между «мгновенной» высотой звука и высотой ближайшего тона отображающего звукоряда. Замена мгновенных высот звуковысотного рисунка высотами ближайших ступеней отображающего звуко­ряда есть, по существу, операция округления. 

Как известно, ее величина не может быть больше половины интервала I₀ между сосед­ними «разрешенными» уровнями значений — в данном случае ступенями: ε ^max = I₀ / 2. Для примера, приведенного на рис. 1, интервал между ступенями I₀ = 100 центам, и максимально возможное несовпадение высот составляет ε ^max = I₀ / 2 = 50 центов. При исследо­вании традиционных музыкальных культур такой уровень погрешности представления может оказаться неприемлемым, поскольку в них встречаются звуковысотные структуры, содержащие от 15 до 30 и более ступе­ней в пересчете на октаву, что соответствует интер­валам от 40 до 80 центов (см., на­пример, [9]).

Теоретическая максимально возможная погрешность ε ^max обычно реализуется весьма редко и потому не вполне адекватно характеризует качество приближения. Более реалистичной является оценка, учитывающая среднее качество аппроксимации по всем мгновенным высотам звуковысотного рисун­ка, а именно, среднеквадратичная погрешность ε ^ср (она широко используется в задачах аппроксимации в науке и технике)3.

Аналогичным образом строится оценка точности отображения длительностей в принятой системе нотировки. Округление моментов начала и окончания тонов до ближайших границ выбранных «единиц времени» ∆t приводит к возможной погрешности по времени не более ∆t /2. Эта погрешность имеет случайный характер, и ее величину можно оценивать среднеквадратичным отклонением фиксируемых длительностей от исходных. В качестве «единицы времени» — наименьшей длительности звука, которую следует нотировать, в [7] предлагалась величина около 60 мс, что соответствует 1/32 для темпа 120 уда­ров в минуту. (При такой длительности звука и шаге анализа 5 мс моменты начала и окончания звука определяются с погрешностью около 8%, а при 30 мс, то есть 1/64, — уже около 16%, что неприемлемо.) Наличие погрешности по времени наступления событий вызывает появление дополнительной погрешности в представлении звуковысотного рисунка.

Хотя знаковая запись требует точного выдерживания высоты тонов и их длительности, в реальной фонограмме эти требования могут существенно нарушаться (например, практически всегда — в вокальном исполнении). В связи с этим требуется доопределить понятие «тона», задав для него допустимые границы изменения по высоте и вариаций по длительности — такие, в пределах которых музыковед-исследователь «согласен» считать высоту тона «практически неизменной», равной фиксируемой в нотировке и длительность — «практически равной» той, которая записывается в нотировке. При этом «тон», будет отображаться в мелограмме не бесконечно тонкой линией на определенной высоте с известной длиной по временной шкале, а «полоской» с некоторой шириной (по шкале высоты) и длиной (по времени), причем внутри полоски возможны разные траектории изменения высоты — но все они будут описываться в нотировке одним и тем же «тоном»4.

В немногочисленных работах зарубежных авторов, рассматривающих задачу нотировки мелограммы в ситуации существенно неточного выдерживания высот и длительностей, обсуждаются аналогичные подходы. Так, в статье [13] проведено статистическое исследование мелодических микротоновых «украшений», используемых в индийской карнатической музыке, с целью построения ее математических моделей. В их теории выделяются «тоны постоянной высоты», то есть звуки, высота которых не изменяется относительно их среднего значения более чем на ∆ полутонов за время C ^min, и «украшения» — быстрые вариации вокруг этих зву­ков. Тоном постоянной высоты считается фрагмент мелограммы, в котором допускаются изменения высоты не более чем на заданную величину за определенное время. Эти параметры выбраны интуитивно: установлен допуск по вы­соте ∆ =0,3 полутона и длительность не ме­нее t ^min = 80..87 мс. Авторы разъясняют, что 80..87 мс — это длительность самого короткого звука, который исполняется без украшений (при таком темпе их невозможно было бы воспринять слушателю). При выделении тонов постоянной высоты проверяется также крутизна изменения высоты в пределах тона: авторы посчитали допустимым изменение не быстрее чем на полутон в секунду — иначе тон следует разбивать на несколько последовательных. В указанной работе понятие тона постоянной высоты применяется при анализе хода мелограммы для разбиения ее на ноти­руемые фрагменты.

Равномерно-темперированный отображающий звукоряд

Одним из распространенных методов представления мелодии является нотирование с помощью равномерно-темперированных отображающих звукорядов с тем или иным числом N ^рт ступеней в октаве, разделенных интервалами I₀ = 1200 / N ^рт центов. Этот интервал служит единицей измерения реальных высот и интервалов в фонограм­ме; чем меньше I₀, тем точнее будет их фик­сация. Максимальная погрешность при N ^рт рав­ноотстоящих ступенях не превышает ε ^max ≤ I₀ / 2 = 600 N ^рт . В европейской академической музыке обычно N ^рт = 12 то есть I₀ = 100 центам; также применяются равномерно-темперированные звукоряды со значительно бóльшим числом ступеней в октаве — до 96 и более, и для них разработаны специальные системы нотации [3].

Рассмотрим задачу подбора «оптимальной» равномерно-темперированной системы для нотирования произвольной фонограммы. Очевидно, что рост числа N ^рт в целом приводит к уменьшению погрешности; ее минимум достигается при максимальном технически возможном числе N ^рт. Однако число ступеней связано с числом знаков (или их комбинаций), необходимых для запи­си всех высот ступеней звукоряда, и слишком большое их число неудобно на практике. 

Кроме того, нет смысла требовать, чтобы погрешность была меньше величины 4–5 центов, характеризующей точность определения высот (как программой, так и человеком; см. выше). Задавшись максимально возможной погрешностью ε ^max, можно вычислить ми­ни­мально требуемое число ступеней, при котором погрешность не превышает ε ^max : N ^min = 600/ε ^max . Например, для требо­ва­ния ε ^max ≤ 10 центов получаем N ^min ≥ 60 сту­пеней в октаве, для ε ^max ≤ 5 центов требу­ется N ^рт не менее 120.

Рассчитать аналогичным простым способом среднеквадратичную погрешность не представляется возможным в силу сложного механизма ее формирования. Для определения числа ступеней в октаве, при котором выполняется условие «среднеквадратичная погрешность не больше заданной», можно только проводить численный эксперимент, то есть пробовать все возможные варианты равномерных звукорядов с разными N и каждый раз вычислять получившуюся для данной мелограммы погрешность. Далее по результатам анализа выбирается подхо­дящий отображающий звукоряд. (Задачу перебора вариантов можно «поручить» со­от­ветствующей компьютерной программе — например SPAX — и полностью автоматизи­ровать процесс анализа; на современном компьютере он занимает около 1–2 секунд при переборе значений N от 10 до 100 для длительности фонограммы около 20 минут.) При этом на погрешность влияет также величина «единицы времени», выбранной для нотирования.

Собственный звукоряд исполнителя

Реальный звукоряд исполнителя выявляется на основе статистического анализа звуковысотного рисунка (см., например, [4; 5, гл. 3; 6]). Для этого весь звуковысотный диапазон фонограммы делится на «окна» (в программе SPAX — шириной в 5 центов) и оценивается время пребывания высоты звука в каждом из «окон», то есть строится гистограмма высот звука. Далее по ней выявляются высоты, которыми преимущественно (по сумме времени звучания) пользуется исполнитель — они и составляют звукоряд, пригодный для нотирования.

На рис. 2 показан фрагмент звуковысот­ной расшифровки и иллюстрируется процесс анализа собственного звукоряда испол­нителя в программе SPAX. Вверху расположен график интенсивности звука; ниже, в ос­новном окне программы, — вычисленная звуковысотная линия, то есть мелограмма. Справа на нее наложен график гистограммы высот — он изображается горизонтальными отрезками с длиной, пропорциональной суммарному времени звучания на данной высоте. Отбор высот ступеней производится по признаку достаточно долгого (в сумме) использования данной высоты, для чего назначается порог минимального суммарного времени звучания T^h (показанный вертикальной линией на рис. 2). Задается также минимально допустимый интервал между ступенями Q ^min . При интервале меньшем Q ^min ступени объединяются (подробнее о методе выявления ступеней звукоряда см. [4; 5, гл. 3]). На рис. 2 выявленные ступени звукоряда отображаются толстыми горизонтальными линиями в левой части нижнего окна.

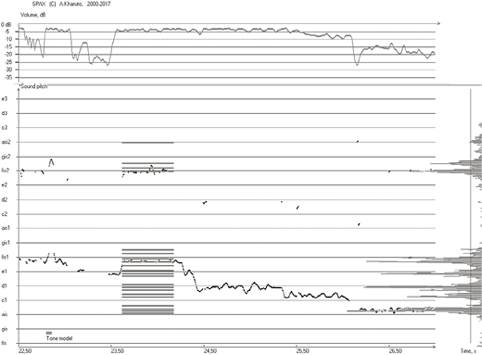
Рис. 2. Пример мелограммы и оценка звукоряда в программе SPAX на основе статистического анализа времени звучания на разных высотах (казахское народное пение)
Fig. 2. Example of a melogram and pitch range assessment in the SPAX program based on statistical analysis of the sound time at different pitch levels (Kazakh folk singing)

Очевидно, что состав выявленной системы ступеней зависит от свойств мелограммы и параметров метода исследования T^h и Q ^min . Значения T^h около 12..15 мс соответствуют самым коротким воспринимаемым человеком тонам определенной высоты [2, 71]; увеличение порога T^h может приводить к уменьше­нию числа зарегистрированных ступеней N ^s . 

По мере увеличения Q ^min все больше соседних ступеней признаются «слишком близкими» и попарно объединяются, что также уменьшает число N ^s (см. подробнее [6]).

Аналогичный подход к выявлению звукоряда, основанный на статистическом анализе высоты звука, используется для нотировки и зарубежными исследователями (см., например, [5, гл. 4; 12]); более точное исследование гистограммы высот применяется при анализе, например, музыки Ближнего Востока [11], Средней Азии и других регионов мира. Так, в работе [10] рассматривается возможность обнаружения в фонограмме раги элементов, характерных для другого лада, на основе характерного распределения высот. В данном случае высота звука определялась на интервалах в 10 мс и полученные частоты приводились к одной октаве; далее вычислялась гистограмма высот. По суммарному времени звучания на данной высоте оценивалась ее «значимость». Затем устанавливались стабильные ладовые структуры (свара) — для этого гистограмма преобразовывалась в сово­купность полос шириной по 35 центов, расположенных около пиков распределения высот. Полосы, для которых суммарная длительность использования оказывалась меньше 250 мс, отбрасывались как малоинформативные. Для распознавания определенной раги производился анализ нескольких ее исполнений, и результаты накапливались в гистограмме для последующего «обучения» программы. Описанный подход аналогичен предлагаемому автором, однако не ставит целью нотировку и оценку ее точности.

Сопоставление результатов аппроксимации при различных звукорядах

Конечная цель — нотировка фонограммы — достигается в два этапа: сначала выполня­ется приемлемая аппроксимация мелограммы, а за­тем происходит преобразование мело­граммы в знаковую последовательность. Первый этап имеет объективный характер и осуществляется, как правило, с помощью компьютерной программы; второй является чисто музыковедческой задачей и трудно формализуется, особенно в случае исследования традиционных музыкальных культур (этот этап в данной статье не рассматривается). Рассмотрим характерные результаты, получаемые на первом этапе анализа, при использовании двух типов звукоряда для одних и тех же фонограмм.

При анализе равномерно-темперирован­ного ряда производится перебор вариантов числа ступеней в октаве N ^рт в пределах от 10 до 100 и вычисляется погрешность ε для каждого N ^рт. (При каждом N ^рт находится оптимальная «настройка» начала звукоряда относительно мелограммы, которая минимизирует погрешность.) В случае использования собственного звукоряда исполнителя производится перебор вариантов сочетания параметров T^h (от 10 до 750 мс с шагом 10 мс) и Q ^min (от 10 до 95 центов с шагом 10 центов); при каждом из сочетаний по гистограмме выделяются ступени звукоряда, производится аппроксимация мелограммы последовательностью тонов и оценивается ее погрешность. (Полученное число ступеней собственного звукоряда N ^s в пределах амбитуса фонограммы пересчитывается затем в среднее число ступеней, приходящихся на октаву.) В обоих случаях количество вычислительных операций оказывается весьма значительным, что требует применения компьютера.

Погрешности при аппроксимации возни­кают как вследствие неточности опреде­ления высоты звука компьютерной програм­мой, так и в результате «неидеального» выдерживания высоты тонов во время исполнения. Хотя с ростом числа ступеней в октаве погрешность в целом уменьшается, это не означает возможности бесконечного повышения точности нотировки, поскольку в процессе все более точной аппроксимации сначала будут «отслежены» все тонкие истинные движения мелодической линии, а затем начнется отображение отклонений, возникших за счет собственных погрешностей мелограммы, порожденных при вычислении высоты звука в каждой точке времени. Таким образом, зона погрешности меньше 4..5 центов является малоинформативной.

На рис. 3 показан результат вычисления среднеквадратичной погрешности аппроксимации мелограммы равномерно-темперированным звукорядом с числом ступеней в октаве от 10 до 100. Анализируемая фонограмма представляет собой запись фортепианной пьесы. На графике ясно видны глубокие локальные минимумы погрешности при числе ступеней, равном 12, 24, 36… Соответствующие минимальные погрешности лежат около величины 5 центов. Полученные данные показывают, что для нотировки следует использовать 12-полутоновый равномерно-темперированный звукоряд; при этом среднеквад­ратичная погрешность нотировки составит около 5,5 центов (без учета погрешностей времени; их влияние повышает погрешность на 4..5 центов).

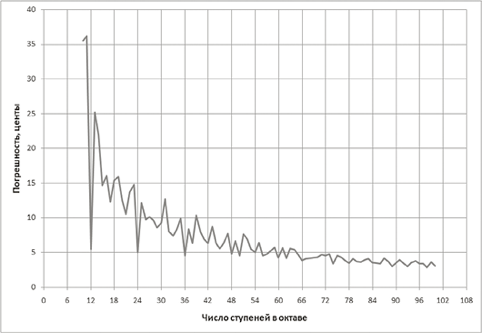
Рис. 3. Пример зависимости погрешности аппроксимации от числа ступеней в октаве для равномерно-темперированного отображающего звукоряда (фортепианное исполнение)
Fig. 3. Example of the dependence of the approximation error on the quantity of steps in an octave for an equally-tempered displaying scale (piano performance)

На рис. 4 показан результат анализа ме­ло­граммы другого инструмента — среднеазиатского тара (это исполнение с точки зрения интервального состава анализировалось в [9]). График погрешности для равномерно-темперированной модели звукоряда похож на полученный для фортепиано — он имеет зигзагообразный вид (штриховая ли­ния). Особенностью игры на таре явля­ется использование плавного глиссандо; поскольку кусочно-постоянная аппроксимация не передает его адекватно, погрешности здесь получаются выше, чем в примере, отоб­раженном на рис. 3. Для равномерно-темперированной модели звукоряда локальные минимумы оказываются выше погрешности в 5 центов вплоть до числа ступеней в октаве, равного 80. При 12 ступенях средне­квадратичная погрешность составляет около 21,5 центов.

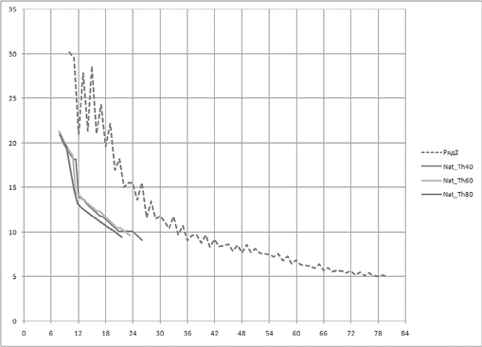
Рис. 4. Зависимость погрешности аппроксимации от числа ступеней в октаве для равномерно-темперированных рядов (штриховая линия) и собственных звукорядов исполнителя (Б. Мансуров, тар, композиция «Шур», 1959 год. Фонограмма из архива В. Н. Юнусовой). «Единица времени» равна 60 мс
Fig. 4. Dependence of the approximation error on the quantity of steps in the octave for equally-tempered scales (dashed line) and the performer’s own scales series (B. Mansurov, tar, composition “Shur,” 1959. Phonogram from the archive of V. N. Yunusova). “Unit of time” is 60 ms

Сплошные линии на рис. 4 показывают графики погрешностей при использовании для аппроксимации собственного звукоряда исполнителя при разных значениях порога времени (цифры после обозначения «Th» в легенде показывают порог в милли­секундах). Из графиков видно, что исполь­зование собственного звукоряда при оди­на­ковом числе ступеней в октаве дает меньшие значения погрешности, чем для рав­номерно-темперированных моделей; для обеспечения равной точности аппроксимации нужно меньшее число ступеней собственного звукоряда. Наибольшая разница достигает 5..8 центов по величине погрешности (при 12..24 ступенях) или около 10..12 ступеней в октаве при равных погрешностях.

Анализ ряда вокальных образцов из разных районов России, а также из стран Ближнего и Дальнего Востока показал, что харак­те­ристики погрешностей в случае приме­не­ния равномерно-темперированного звукоряда как минимум на 3..5 центов хуже аппроксимации собственным звукорядом исполнителя при одинаковом числе ступеней в октаве; при одинаковой точности потребуется значительно больше ступеней равномерно-темперированного звукоряда. Характерный вид семейства кривых приведен на рис. 5 (сплошные линии). Их общее расположение на плоскости графика зависит от исследуемого му­зыкального образца. В приведенном примере (рис. 5) погрешность не более 10 центов достигается, например, при 26 ступенях собственного звукоряда или 44 ступенях равномерно-темперированного. С помощью собственного звукоряда не удастся аппроксимировать мелограмму с погрешностью менее 8 центов при числе ступеней около 30; это объясняется, видимо, множественными отклонениями высоты от ступеней в процессе вокального исполнения. С помощью равномерно-темперированного звукоряда такая точность достигается при числе ступеней около 60.

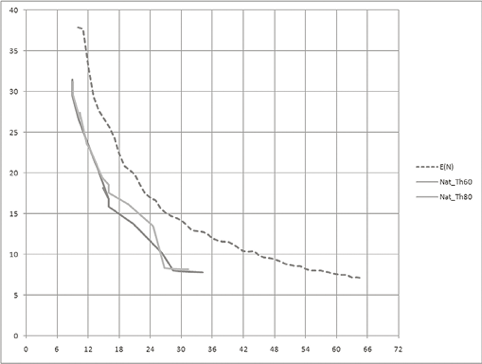
Рис. 5. Зависимость погрешности аппроксимации от числа ступеней в октаве для равномерно-темперированных рядов (штриховая линия) и собственных звукорядов исполнителя (русское народное пение). «Единица времени» равна 60 мс
Fig. 5. The dependence of the approximation error on the quantity of steps in the octave for equally-tempered scales (dashed line) and the performer’s own scales (Russian folk singing). “Unit of time” is 60 ms

Учет выбранной (для измерения длитель­ностей) «единицы времени», до которой производится округление всех моментов времени, также влияет на общий ход графиков, сдвигая их в сторону большей погрешности. Так, переход от «единицы времени» в 10 мс к величине 60 мс приводит к увеличению погрешностей по высоте примерно на 3..5 центов. Собственная погрешность времени при такой «единице времени» характеризуется среднеквадратичным отклонением округлен­ных значений от исходных для разных фонограмм от 17 до 25 мс (что примерно соответствует 1/120..1/80 для темпа 120 ударов в минуту).

Заключение

Таким образом, использование собственного звукоряда исполнителя, выявляемого на основе статистического анализа звуковысотного рисунка, всегда дает более точный результат нотировки, чем применение равномерно-темперированной модели с тем или иным числом ступеней. Достигаемый выигрыш в точности аппроксимации составляет (при исследовании разнородных образцов пения и игры на музыкальных инструментах) от 3 до 8 и более центов. Для обеспечения одинаковой точности требуется меньше ступеней собственного звукоряда, чем равномерно-темперированного; выигрыш составляет до 10..18 и более ступеней.

Программа SPAX выполняет все необходимые вычисления, связанные с решением задач анализа мелограммы и представляет «обзорный» результат для обоих типов звукоряда: таблицу величин погрешностей для равномерно-темперированного звукоряда при числе ступеней в октаве от 10 до 100, а также таблицы числа ступеней собственного звукоряда, построенного на основе гистограммы высот и заданных параметров — порогового времени звучания и минимального расстояния между ступенями; для каждого такого сочетания вычисляется и заносится в таблицу среднеквадратичная погрешность аппроксимации высоты и округления моментов времени.

Численные результаты компьютерного исследования позволяют определить границы точности аппроксимации (которая затем ляжет в основу нотировки) и выбрать тип отображающего звукоряда и число ступеней в нем. Со своей стороны музыковед устанавливает величину погрешности, которую считает приемлемой для описания (нотировки) данного исполнения. В дальнейшем, зная величину погрешности, мы можем (или, напротив, не имеем такой возможности) судить о сходстве мелодических линий, фиксировать с известной точностью звукоряд, исследовать стилевые особенности исполнения с учетом неизбежной погрешности численного анализа.

Список источников

1. Алдошина И., Приттс Р. Музыкальная акустика. СПб. : Композитор, 2006. 720 с.
2. Кузнецов Л. А. Акустика музыкальных инструментов. Справочник. М. : Легпромиздат, 1989. 368 с.
3. Назайкинский Е. В. Проблемы теории и практики экмелической музыки (информационно-аналитический обзор) // Музыка в информационном мире. Наука. Творчество. Педагогика : Сборник научных статей / науч. ред. Г. Р. Тараева, Т. Ф. Шак. Ростов-на-Дону : Издательство Ростовской гос. консерватории им. С. В. Рахманинова, 2004. С. 44–64.
4. Харуто А. В. Компьютерный анализ звукоряда по фонограмме // Музыкальная академия. 2010. № 3. С. 83–89. URL: https://mus.academy/articles/kompyuternyi-analiz-zvukoryada-po-fonogramme (дата обращения: 01.10.2021).
5. Харуто А. Компьютерный анализ звука в музыкальной науке. М. : НИЦ «Московская консерватория», 2015. 448 с.
6. Харуто А. Компьютерный анализ высоты звука в музыковедческом исследовании: информационный аспект // Музыкальная академия. 2016. № 3. С. 98–102.
7. Харуто А. Компьютерный анализ длительностей звуков в музыкальном исполнении // Музыкальная академия. 2017. № 3. С. 125–128.
8. Харуто А. В., Смирнов Д. В. Использование компьютерного анализа в исследовании звуковысотного строения народной музыки // Музыка устной традиции: Материалы международных научных конференций памяти А. В. Рудневой / науч. ред. Н. Н. Гилярова, сост. В. М. Щуров, Н. Н. Гилярова. М. : Московская консерватория ООО «Биоинформсервис», 1999. С. 335–340. (Научные труды Московской государственной консерватории им. П. И. Чайковского, сб. 27).
9. Юнусова В., Харуто А. Компьютерный анализ параметров стиля исполнения в традиционной культуре (на материале классической музыки Востока) // Музыкальная академия. 2015. № 1. С. 143–147.
10. Ganguli K. K., Rao P. Towards Computational Mo­de­ling of the Ungrammatical in a Raga Per­for­mance // Proceedings of 18th International Society for Music Information Retrieval Conference, Suzhou, China, October 23–27, 2017 / ed. by S. J. Cunningham, Zh. Duan, X. Hu, D. Turnbull. Suzhou : [s.n.], 2017. P. 39–45. DOI: 10.5281/zenodo.1417349.
11. Gedik A. C., Bozkurt B. Pitch-frequency histogram-based music information retrieval for Turkish mu­sic // Signal Processing. Vol. 90. Issue 4 (April 2010). P. 1049–1063. DOI: 10.1016/j.sigpro.2009.06.017.
12. Tzanetakis G., Kapur А., Schloss W. A., Wright M. Computational Ethnomusicology // Journal of Interdisciplinary Music Studies. Vol. 1. Issue 2 (Fall 2007). P. 1–24.
13. Viraraghavan V. S., Aravind R., Murthy A. H. A Sta­tistical Analysis of Gamakas in Carnatic Music // Proceedings of the 18th International Society for Music Information Retrieval Conference, Suzhou, China, October 23–27, 2017 / ed. by S. J. Cunningham, Zh. Duan, X. Hu, D. Turnbull. Suzhou: [s.n.], 2017. P. 243–249. DOI: 10.5281/zenodo.1417837.